题目内容
5.下列运算错误的是( )| A. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | B. | 2$\sqrt{2}$+2$\sqrt{3}$=5$\sqrt{5}$ | C. | $\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$ | D. | $\sqrt{{(-4)}^{2}}$=4 |
分析 根据二次根式的乘法法则对A进行判断;利用二次根式的加减法对B进行判断;利用分母有理化对C进行判断;利用二次根式的性质对D进行判断;
解答 解:A、原式=$\sqrt{2×3}$=$\sqrt{6}$,所以A选项的计算正确;
B、2$\sqrt{2}$与2$\sqrt{3}$不能合并,所以B选项的计算错误;
C、原式=$\frac{\sqrt{2}}{2}$,所以C选项的计算正确;
D、原式=4,所以D选项的计算正确.
故选B.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
20.已知y与x成正比例,且当x=2时,y=3,则当y=2时x的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | 3 |
17.使函数y=$\frac{\sqrt{x}}{x+2}$有意义的x的取值范围是( )
| A. | x≠-2 | B. | x≥0 | C. | x>-2 | D. | -2<x≤0 |
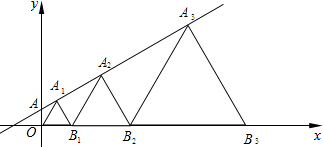 如图,在直线y=$\frac{\sqrt{3}}{3}$x+1上取一点A1,以O、A1为顶点作等一个等边三角形OA1B1,再在直线上取一点A2,以A2、B1为顶点作第二个等边三角形A2B1B2,…,一直这样做下去,则B1点的坐标为($\sqrt{3}$,0),第10个等边三角形的边长为29$\sqrt{3}$.
如图,在直线y=$\frac{\sqrt{3}}{3}$x+1上取一点A1,以O、A1为顶点作等一个等边三角形OA1B1,再在直线上取一点A2,以A2、B1为顶点作第二个等边三角形A2B1B2,…,一直这样做下去,则B1点的坐标为($\sqrt{3}$,0),第10个等边三角形的边长为29$\sqrt{3}$. 如图,函数y=ax+4和y=bx的图象相交于点A,则不等式bx≥ax+4的解集为x≥2.
如图,函数y=ax+4和y=bx的图象相交于点A,则不等式bx≥ax+4的解集为x≥2.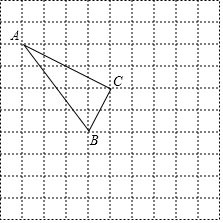 如图,在正方形网格中,每个小正方形的边长为1个单位长度,格点三角形ABC(顶点是网格线的交点的三角形)的顶点A,C的坐标分别为(-4,5),(0,3).
如图,在正方形网格中,每个小正方形的边长为1个单位长度,格点三角形ABC(顶点是网格线的交点的三角形)的顶点A,C的坐标分别为(-4,5),(0,3).