题目内容
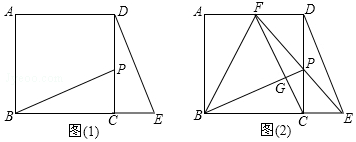
15.如图1,有若干张边长为a的小正方形①、长为b宽为a的长方形②以及边长为b的大正方形③的纸片.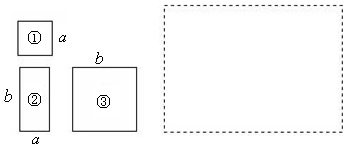
(1)已知小正方形①与大正方形③的面积之和为169,长方形②的周长为34,求长方形②的面积.
(2)如果现有小正方形①1张,大正方形③2张,长方形②3张,请你将它们拼成一个大长方形 (在图2虚线框内画出图形),并运用面积之间的关系,将多项式a2+3ab+2b2分解因式.
分析 (1)根据题意表示出a+b与a2+b2的值,利用完全平方公式求出ab的值,即可确定出所求;
(2)根据题意画出相应的图形,将多项式分解即可.
解答 解:(1)由题意得:a+b=17,a2+b2=169,
∵(a+b)2=a2+b2+2ab∴289=169+2ab,
∴ab=60,
∴长方形②的面积为60;
(2)如图:
∴a2+3ab+2b2=(a+2b)(a+b).
点评 此题考查了因式分解的应用,弄清题意是解本题的关键.

练习册系列答案
相关题目
7.下列说法正确的是( )
| A. | -(-8)的立方根是-2 | B. | 立方根等于本身数有-1,0,1 | ||
| C. | $-\sqrt{64}$的立方根为-4 | D. | 一个数的立方根不是正数就是负数 |
4.关于直线l:y=kx+k(k≠0),下列说法中正确的是( )
| A. | 点(0,-k)在直线l上 | B. | y随x的增大而减小 | ||
| C. | 直线l经过第一、二、三象限 | D. | 直线l经过点(-1,0) |
5.下列运算错误的是( )
| A. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | B. | 2$\sqrt{2}$+2$\sqrt{3}$=5$\sqrt{5}$ | C. | $\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$ | D. | $\sqrt{{(-4)}^{2}}$=4 |
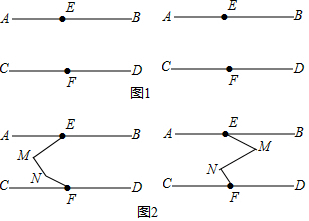
 完成下面的证明.
完成下面的证明.