题目内容
14．若点P（1，b）到x轴的距离为2，则P点坐标为（1，2）或（1，-2）．分析 根据点到x轴的距离等于纵坐标的绝对值列绝对值方程求出b的值，从而得解．
解答 解：∵点P（1，b）到x轴的距离为2，
∴|b|=2，
解得b=±2，
∴P点坐标为（1，2）或（1，-2）．
故答案为：（1，2）或（1，-2）．
点评 本题考查了点的坐标，熟记点到x轴的距离等于纵坐标的绝对值是解题的关键．
练习册系列答案
相关题目
4．关于直线l：y=kx+k（k≠0），下列说法中正确的是（ ）
| A． | 点（0，-k）在直线l上 | B． | y随x的增大而减小 | ||
| C． | 直线l经过第一、二、三象限 | D． | 直线l经过点（-1，0） |
5．下列运算错误的是（ ）
| A． | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | B． | 2$\sqrt{2}$+2$\sqrt{3}$=5$\sqrt{5}$ | C． | $\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$ | D． | $\sqrt{{（-4）}^{2}}$=4 |
2．$\sqrt{9}$所表示的是（ ）
| A． | 9的平方根 | B． | 3的平方根 | C． | 9的算术平方根 | D． | 3的算术平方根 |
9．
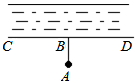如图，计划把河水引到水池A中，先作AB⊥CD，垂足为B，然后沿AB开渠，能使所开的渠道最短，这样设计的数学根据是（ ）
如图，计划把河水引到水池A中，先作AB⊥CD，垂足为B，然后沿AB开渠，能使所开的渠道最短，这样设计的数学根据是（ ）| A． | 两点之间，线段最短 | |
| B． | 两条平行线之间的距离处处相等 | |
| C． | 经过直线上或直线外一点，有且只有一条直线与已知直线垂直 | |
| D． | 直线外一点与直线上各点连接的所有线段中，垂线段最短 |
6．以下列各组长度的线段为边，能构成三角形的是（ ）
| A． | 8，4，4 | B． | 5，6，12 | C． | 6，8，10 | D． | 1，2，3 |
3．
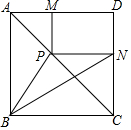如图，正方形ABCD的对角线上一动点P，作PM⊥AD于点M，PN⊥CD于点N，连接BP，BN，若AB=3，BP=$\sqrt{5}$，则BN的长为（ ）
如图，正方形ABCD的对角线上一动点P，作PM⊥AD于点M，PN⊥CD于点N，连接BP，BN，若AB=3，BP=$\sqrt{5}$，则BN的长为（ ）| A． | $\sqrt{15}$ | B． | $\sqrt{13}$或$\sqrt{10}$ | C． | 4 | D． | 5 |