题目内容
20.已知y与x成正比例,且当x=2时,y=3,则当y=2时x的值为( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | 3 |
分析 根据正比例函数的概念设出其解析式,把x=2时,y=3代入即可.
解答 解:设y=kx,
把当x=2时,y=3,代入得:k=$\frac{3}{2}$,
故此函数的解析式为:y=$\frac{3}{2}$x,
所以当Y=2时,则2=$\frac{3}{2}$x,
解得x=$\frac{4}{3}$,
故选B.
点评 本题考查的是用待定系数法求正比例函数的解析式,比较简单.

练习册系列答案
相关题目
11.有下列命题:①若a>b,则a-b>0;②若a>b>c>0,则ac>bc;③若$\frac{a}{2}$-3>$\frac{b}{2}$-3,则a<b;④若a<b<0,则$\frac{a}{b}$>1.其中真命题有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.下列运算错误的是( )
| A. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | B. | 2$\sqrt{2}$+2$\sqrt{3}$=5$\sqrt{5}$ | C. | $\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$ | D. | $\sqrt{{(-4)}^{2}}$=4 |
9.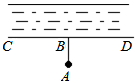 如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的数学根据是( )
如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的数学根据是( )
 如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的数学根据是( )
如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的数学根据是( )| A. | 两点之间,线段最短 | |
| B. | 两条平行线之间的距离处处相等 | |
| C. | 经过直线上或直线外一点,有且只有一条直线与已知直线垂直 | |
| D. | 直线外一点与直线上各点连接的所有线段中,垂线段最短 |
10.在菱形ABCD中,若AB=2,则菱形的周长为( )
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
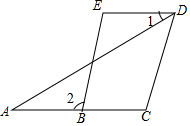 完成下面的证明.
完成下面的证明.