题目内容
10.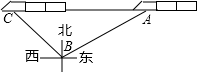 如图,在距离铁轨200米的B处,观察由南宁开往百色的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东60°方向上;10秒钟后,动车车头到达C处,恰好位于B处的西北方向上,则这时段动车的平均速度是( )米/秒.
如图,在距离铁轨200米的B处,观察由南宁开往百色的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东60°方向上;10秒钟后,动车车头到达C处,恰好位于B处的西北方向上,则这时段动车的平均速度是( )米/秒.| A. | 20($\sqrt{3}$+1) | B. | 20($\sqrt{3}$-1) | C. | 200 | D. | 300 |
分析 作BD⊥AC于点D,在Rt△ABD中利用三角函数求得AD的长,在Rt△BCD中,利用三角函数求得CD的长,则AC即可求得,进而求得速度.
解答 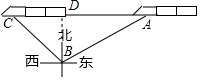 解:作BD⊥AC于点D.
解:作BD⊥AC于点D.
∵在Rt△ABD中,∠ABD=60°,
∴AD=BD•tan∠ABD=200$\sqrt{3}$(米),
同理,CD=BD=200(米).
则AC=200+200$\sqrt{3}$(米).
则平均速度是$\frac{200+200\sqrt{3}}{10}$=20($\sqrt{3}$+1)米/秒.
故选A.
点评 此题考查了解直角三角形及勾股定理的应用,用到的知识点是方向角,关键是根据题意画出图形,作出辅助线,构造直角三角形,“化斜为直”是解三角形的基本思路,常需作垂线(高),原则上不破坏特殊角.

练习册系列答案
相关题目
20.下列计算正确的是( )
| A. | 3m-m=2 | B. | m4÷m3=m | C. | (-m2)3=m6 | D. | -(m-n)=m+n |
5.化简:|-15|等于( )
| A. | 15 | B. | -15 | C. | ±15 | D. | $\frac{1}{15}$ |
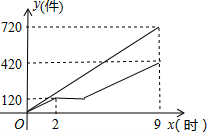 甲、乙两车间同时开始加工一批服装.从开始加工到加工完这批服装甲车间工作了9小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为y(件).甲车间加工的时间为x(时),y与x之间的函数图象如图所示.
甲、乙两车间同时开始加工一批服装.从开始加工到加工完这批服装甲车间工作了9小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为y(件).甲车间加工的时间为x(时),y与x之间的函数图象如图所示.