题目内容
1.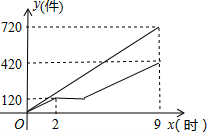 甲、乙两车间同时开始加工一批服装.从开始加工到加工完这批服装甲车间工作了9小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为y(件).甲车间加工的时间为x(时),y与x之间的函数图象如图所示.
甲、乙两车间同时开始加工一批服装.从开始加工到加工完这批服装甲车间工作了9小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为y(件).甲车间加工的时间为x(时),y与x之间的函数图象如图所示.(1)甲车间每小时加工服装件数为80件;这批服装的总件数为1140件.
(2)求乙车间维修设备后,乙车间加工服装数量y与x之间的函数关系式;
(3)求甲、乙两车间共同加工完1000件服装时甲车间所用的时间.
分析 (1)根据工作效率=工作总量÷工作时间,即可求出甲车间每小时加工服装件数,再根据这批服装的总件数=甲车间加工的件数+乙车间加工的件数,即可求出这批服装的总件数;
(2)根据工作效率=工作总量÷工作时间,即可求出乙车间每小时加工服装件数,根据工作时间=工作总量÷工作效率结合工作结束时间,即可求出乙车间修好设备时间,再根据加工的服装总件数=120+工作效率×工作时间,即可求出乙车间维修设备后,乙车间加工服装数量y与x之间的函数关系式;
(3)根据加工的服装总件数=工作效率×工作时间,求出甲车间加工服装数量y与x之间的函数关系式,将甲、乙两关系式相加令其等于1000,求出x值,此题得解.
解答 解:(1)甲车间每小时加工服装件数为720÷9=80(件),
这批服装的总件数为720+420=1140(件).
故答案为:80;1140.
(2)乙车间每小时加工服装件数为120÷2=60(件),
乙车间修好设备的时间为9-(420-120)÷60=4(时).
∴乙车间维修设备后,乙车间加工服装数量y与x之间的函数关系式为y=120+60(x-4)=60x-120(4≤x≤9).
(3)甲车间加工服装数量y与x之间的函数关系式为y=80x,
当80x+60x-120=1000时,x=8.
答:甲、乙两车间共同加工完1000件服装时甲车间所用的时间为8小时.
点评 本题考查了一次函数的应用以及解一元一次方程,解题的关键是:(1)根据数量关系,列式计算;(2)根据数量关系,找出乙车间维修设备后,乙车间加工服装数量y与x之间的函数关系式;(3)根据数量关系,找出甲车间加工服装数量y与x之间的函数关系式.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
6.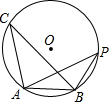 如图,△ABC是⊙O的内接三角形,∠C=30°,⊙O的半径为5,若点P是⊙O上的一点,在△ABP中,PB=AB,则PA的长为( )
如图,△ABC是⊙O的内接三角形,∠C=30°,⊙O的半径为5,若点P是⊙O上的一点,在△ABP中,PB=AB,则PA的长为( )
 如图,△ABC是⊙O的内接三角形,∠C=30°,⊙O的半径为5,若点P是⊙O上的一点,在△ABP中,PB=AB,则PA的长为( )
如图,△ABC是⊙O的内接三角形,∠C=30°,⊙O的半径为5,若点P是⊙O上的一点,在△ABP中,PB=AB,则PA的长为( )| A. | 5 | B. | $\frac{5\sqrt{3}}{2}$ | C. | 5$\sqrt{2}$ | D. | 5$\sqrt{3}$ |
13.大美山水“硒都•恩施”是一张亮丽的名片,八方游客慕名而来,今年“五•一”期间,恩施州共接待游客1450000人,将1450000用科学记数法表示为( )
| A. | 0.145×106 | B. | 14.5×105 | C. | 1.45×105 | D. | 1.45×106 |
10.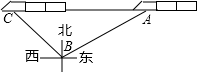 如图,在距离铁轨200米的B处,观察由南宁开往百色的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东60°方向上;10秒钟后,动车车头到达C处,恰好位于B处的西北方向上,则这时段动车的平均速度是( )米/秒.
如图,在距离铁轨200米的B处,观察由南宁开往百色的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东60°方向上;10秒钟后,动车车头到达C处,恰好位于B处的西北方向上,则这时段动车的平均速度是( )米/秒.
 如图,在距离铁轨200米的B处,观察由南宁开往百色的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东60°方向上;10秒钟后,动车车头到达C处,恰好位于B处的西北方向上,则这时段动车的平均速度是( )米/秒.
如图,在距离铁轨200米的B处,观察由南宁开往百色的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东60°方向上;10秒钟后,动车车头到达C处,恰好位于B处的西北方向上,则这时段动车的平均速度是( )米/秒.| A. | 20($\sqrt{3}$+1) | B. | 20($\sqrt{3}$-1) | C. | 200 | D. | 300 |
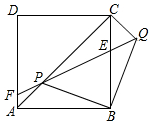 边长为2$\sqrt{2}$的正方形ABCD中,P是对角线AC上的一个动点(点P与A、C不重合),连接BP,将BP绕点B顺时针旋转90°到BQ,连接QP,QP与BC交于点E,QP延长线与AD(或AD延长线)交于点F.
边长为2$\sqrt{2}$的正方形ABCD中,P是对角线AC上的一个动点(点P与A、C不重合),连接BP,将BP绕点B顺时针旋转90°到BQ,连接QP,QP与BC交于点E,QP延长线与AD(或AD延长线)交于点F.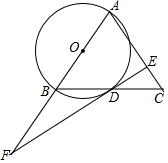 如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作⊙O的切线DE交AC于点E,交AB延长线于点F.
如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作⊙O的切线DE交AC于点E,交AB延长线于点F.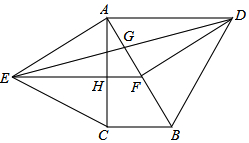 如图,分别以Rt△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB边的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.
如图,分别以Rt△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB边的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.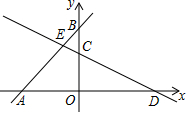 如图,直线y=mx+3与x轴、y轴交于点A、点B,直线CD与x轴交于点D,与y轴交于点C(0,2),与直线AB交于点E,点E的坐标为(-$\frac{2}{3}$,$\frac{7}{3}$).
如图,直线y=mx+3与x轴、y轴交于点A、点B,直线CD与x轴交于点D,与y轴交于点C(0,2),与直线AB交于点E,点E的坐标为(-$\frac{2}{3}$,$\frac{7}{3}$).