题目内容
14.化简(求值)(1)$\frac{a+b}{a-b}$+$\frac{a}{b-a}$
(2)$\frac{a-1}{{a}^{2}-4a+4}$×$\frac{{a}^{2}-4}{2a-2}$,其中a=-1.
分析 (1)根据分式的运算法则即可求出答案
(2)先将分式化简,然后将a代入即可求出答案.
解答 解:(1)原式=$\frac{a+b}{a-b}-\frac{a}{a-b}$=$\frac{a}{a-b}$
(2)原式=$\frac{a-1}{(a-2)^{2}}×\frac{(a+2)(a-2)}{2(a-1)}$
=$\frac{a+2}{2(a-2)}$
当a=-1时,
∴原式=$\frac{-1+2}{2×(-3)}$=$-\frac{1}{6}$
点评 本题考查分式的运算法则,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
相关题目
10.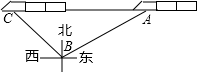 如图,在距离铁轨200米的B处,观察由南宁开往百色的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东60°方向上;10秒钟后,动车车头到达C处,恰好位于B处的西北方向上,则这时段动车的平均速度是( )米/秒.
如图,在距离铁轨200米的B处,观察由南宁开往百色的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东60°方向上;10秒钟后,动车车头到达C处,恰好位于B处的西北方向上,则这时段动车的平均速度是( )米/秒.
 如图,在距离铁轨200米的B处,观察由南宁开往百色的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东60°方向上;10秒钟后,动车车头到达C处,恰好位于B处的西北方向上,则这时段动车的平均速度是( )米/秒.
如图,在距离铁轨200米的B处,观察由南宁开往百色的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东60°方向上;10秒钟后,动车车头到达C处,恰好位于B处的西北方向上,则这时段动车的平均速度是( )米/秒.| A. | 20($\sqrt{3}$+1) | B. | 20($\sqrt{3}$-1) | C. | 200 | D. | 300 |
3. 如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC.若AB=m,AD=n,则四边形OCED的面积为( )
如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC.若AB=m,AD=n,则四边形OCED的面积为( )
 如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC.若AB=m,AD=n,则四边形OCED的面积为( )
如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC.若AB=m,AD=n,则四边形OCED的面积为( )| A. | mn | B. | $\frac{1}{2}$mn | C. | $\frac{1}{4}$mn | D. | $\sqrt{mn}$ |
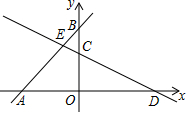 如图,直线y=mx+3与x轴、y轴交于点A、点B,直线CD与x轴交于点D,与y轴交于点C(0,2),与直线AB交于点E,点E的坐标为(-$\frac{2}{3}$,$\frac{7}{3}$).
如图,直线y=mx+3与x轴、y轴交于点A、点B,直线CD与x轴交于点D,与y轴交于点C(0,2),与直线AB交于点E,点E的坐标为(-$\frac{2}{3}$,$\frac{7}{3}$). 如图,⊙O的直径AB=4,BC切⊙O于点B,OC平行于弦AD,OC=5,则AD的长为$\frac{8}{5}$.
如图,⊙O的直径AB=4,BC切⊙O于点B,OC平行于弦AD,OC=5,则AD的长为$\frac{8}{5}$. 已知∠D=∠A,∠B=∠FCB,求证:∠D=∠DCF.
已知∠D=∠A,∠B=∠FCB,求证:∠D=∠DCF. 如图,在矩形ABCD中,对角线AC、BD交于点O,将△ABC沿直线AC翻折,点B落在点B′处,且AB′∥BD,连接B′D.
如图,在矩形ABCD中,对角线AC、BD交于点O,将△ABC沿直线AC翻折,点B落在点B′处,且AB′∥BD,连接B′D.