题目内容
已知点A(1,-1)在反比例函数y=
的图象上,过点A作AM⊥x轴于点M,则△OAM的面积为( )
| -1 |
| x |
A、
| ||
| B、2 | ||
| C、1 | ||
D、
|
考点:反比例函数系数k的几何意义
专题:
分析:直接根据反比例函数y=
(k≠0)系数k的几何意义求解.
| k |
| x |
解答:解:∵AC⊥x轴于点B,
∴△MAO的面积=
|k|=
×1=
.
故选D.
∴△MAO的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选D.
点评:本题考查了反比例函数y=
(k≠0)系数k的几何意义:从反比例函数y=
(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.
| k |
| x |
| k |
| x |

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 某班有男生30人,女生20人.下图分别是该班男、女生参加体育锻炼项目人数的扇形统计图.根据统计图,该班参加体育锻炼人数最多的项目是( )
某班有男生30人,女生20人.下图分别是该班男、女生参加体育锻炼项目人数的扇形统计图.根据统计图,该班参加体育锻炼人数最多的项目是( )| A、跳绳 | B、引体向上 |
| C、跳远 | D、仰卧起坐 |
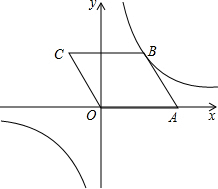 如图,在平面直角坐标系中,□ABCO的顶点A、C的坐标分别为A (2,0)、C (-1,2),反比例函数y=
如图,在平面直角坐标系中,□ABCO的顶点A、C的坐标分别为A (2,0)、C (-1,2),反比例函数y= 如图,在Rt△ABC中,∠ACB=90°,AC=3cm,BC=4cm.动点P从点B出发,以每秒1cm的速度沿射线BA运动,求出点P运动所有的时间t,使得△PBC为等腰三角形.
如图,在Rt△ABC中,∠ACB=90°,AC=3cm,BC=4cm.动点P从点B出发,以每秒1cm的速度沿射线BA运动,求出点P运动所有的时间t,使得△PBC为等腰三角形.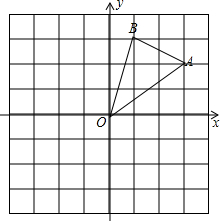 如图,在边长为1的正方形组成的网格中,△AOB的顶点圴在格点上,其中A(3,2)、B(1,3)
如图,在边长为1的正方形组成的网格中,△AOB的顶点圴在格点上,其中A(3,2)、B(1,3)
 如图,已知点D在点O的北偏西30°方向,点E在点O的北偏东50°方向,那么∠DOE的度数为
如图,已知点D在点O的北偏西30°方向,点E在点O的北偏东50°方向,那么∠DOE的度数为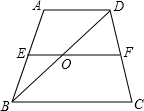 如图,在梯形ABCD中,AD∥BC,中位线EF交BD于点O,若FO-EO=6,则BC-AD为
如图,在梯形ABCD中,AD∥BC,中位线EF交BD于点O,若FO-EO=6,则BC-AD为