题目内容
 如图,在Rt△ABC中,∠ACB=90°,AC=3cm,BC=4cm.动点P从点B出发,以每秒1cm的速度沿射线BA运动,求出点P运动所有的时间t,使得△PBC为等腰三角形.
如图,在Rt△ABC中,∠ACB=90°,AC=3cm,BC=4cm.动点P从点B出发,以每秒1cm的速度沿射线BA运动,求出点P运动所有的时间t,使得△PBC为等腰三角形.考点:等腰三角形的判定,勾股定理
专题:动点型
分析:根据勾股定理求出斜边AB,根据等腰三角形的判定得出符合情况的三种情况:①BP=PC,②BP=BC,③BC=CP,根据等腰三角形的性质得出即可.
解答:解:在Rt△ABC中,∠ACB=90°,AC=3cm,BC=4cm,
∴AB=5cm,
由运动可知,BP=t,且△PBC为等腰三角形有三种可能:
①若BP=PC,则∠B=∠PCB,
∵∠ACB=90°,
∴∠PAC=∠PCA,
∴PC=PA,
∴t=BP=
AB=
;
②若BP=BC,则t=4;
③若BC=PC,过点C作CH⊥AB,如图,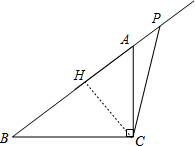
则BP=2BH.由CH×AB=BC×AC,得CH=
;
在Rt△BHC中,由勾股定理得BH=
,
∴t=BP=
;
综上所述,符合要求的t的值有3个,分别是
秒或4秒
秒.
∴AB=5cm,
由运动可知,BP=t,且△PBC为等腰三角形有三种可能:
①若BP=PC,则∠B=∠PCB,
∵∠ACB=90°,
∴∠PAC=∠PCA,
∴PC=PA,
∴t=BP=
| 1 |
| 2 |
| 5 |
| 2 |
②若BP=BC,则t=4;
③若BC=PC,过点C作CH⊥AB,如图,

则BP=2BH.由CH×AB=BC×AC,得CH=
| 12 |
| 5 |
在Rt△BHC中,由勾股定理得BH=
| 16 |
| 5 |
∴t=BP=
| 32 |
| 5 |
综上所述,符合要求的t的值有3个,分别是
| 5 |
| 2 |
| 32 |
| 5 |
点评:本题考查了等腰三角形的性质和判定,勾股定理,三角形的面积的应用,能求出符合情况的所有情况是解此题的关键,用了分类讨论思想.

练习册系列答案
相关题目
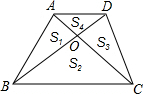 如图,已知在梯形ABCD中,AD∥BC,BC=2AD,如果对角线AC与BD相交于点O,△AOB、△BOC、△COD、△DOA的面积分别记作S1、S2、S3、S4,那么下列结论中,不正确的是( )
如图,已知在梯形ABCD中,AD∥BC,BC=2AD,如果对角线AC与BD相交于点O,△AOB、△BOC、△COD、△DOA的面积分别记作S1、S2、S3、S4,那么下列结论中,不正确的是( )| A、S1=S3 |
| B、S2=2S4 |
| C、S2=2S1 |
| D、S1•S3=S2•S4 |
若a是有理数,则计算正确的是( )
| A、3a-a=3 |
| B、a-(-a)=0 |
| C、a+(-a)=2a |
| D、-a-a=-2a |
已知点A(1,-1)在反比例函数y=
的图象上,过点A作AM⊥x轴于点M,则△OAM的面积为( )
| -1 |
| x |
A、
| ||
| B、2 | ||
| C、1 | ||
D、
|
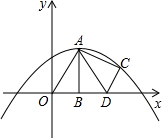 如图,已知△ABO中,点B在x轴上,∠ABO=90°,点A(1,
如图,已知△ABO中,点B在x轴上,∠ABO=90°,点A(1, 作出如图立体图形的三视图.
作出如图立体图形的三视图.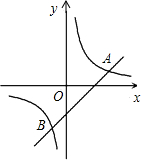 如图,点A是反比例函数y=
如图,点A是反比例函数y=