题目内容
在平面直角坐标系中,已知△AOB的顶点A(-3,2),B(0,2),O为坐标原点,先将△AOB绕着点O顺时针旋转90°,得到△COD,再将△COD向右平移m(m>0)个单位,得到△EFH.
(1)求C,D的坐标.
(2)若反比例函数y=
(k≠0)的图象经过点C及EF的中点M,求反比例函数的解析式及m的值.
(3)在(2)的条件下,连接CE,求四边形OFEC的面积.
(1)求C,D的坐标.
(2)若反比例函数y=
| k |
| x |
(3)在(2)的条件下,连接CE,求四边形OFEC的面积.
考点:反比例函数综合题,平行四边形的判定与性质,平移的性质,旋转的性质
专题:综合题
分析:(1)只需运用旋转的性质就可解决问题;
(2)只需运用待定系数法就可求出反比例函数的解析式,然后结合平移的性质得到点E、F的坐标(用m的代数式表示),然后根据中点坐标公式得到点M的坐标(用m的代数式表示),然后把点M的坐标代入反比例函数的解析式,就可求出m的值;
(3)由平移的性质可得四边形OFEC是平行四边形,然后运用平行四边形的面积公式就可解决问题.
(2)只需运用待定系数法就可求出反比例函数的解析式,然后结合平移的性质得到点E、F的坐标(用m的代数式表示),然后根据中点坐标公式得到点M的坐标(用m的代数式表示),然后把点M的坐标代入反比例函数的解析式,就可求出m的值;
(3)由平移的性质可得四边形OFEC是平行四边形,然后运用平行四边形的面积公式就可解决问题.
解答:解:(1)∵A(-3,2),B(0,2),
∴AB=3,OB=2,∠ABO=90°.
∵△COD是由△AOB绕着点O顺时针旋转90°所得,
∴OD=OB=2,CD=AB=3,∠CDO=∠ABO=90°,
∴点C的坐标为(2,3),点D的坐标为(2,0);
(2)∵反比例函数y=
(k≠0)的图象经过点C,
∴k=2×3=6,
∴反比例函数的解析式为y=
.
∵△EFH是由△COD向右平移m(m>0)个单位所得,
∴点E的坐标为(2+m,3),点F的坐标为(m,0).
∴EF的中点M坐标为(
,
),即(1+m,
).
∵反比例函数y=
的图象经过点M(1+m,
),
∴
(1+m)=6,
解得:m=3,
∴m的值为3;
(3)由平移的性质可得:OF=CE,OF∥CE,
∴四边形OFEC是平行四边形,
∴S?OFEC=OF•EH=3×3=9,
即四边形OFEC的面积为9.
∴AB=3,OB=2,∠ABO=90°.
∵△COD是由△AOB绕着点O顺时针旋转90°所得,
∴OD=OB=2,CD=AB=3,∠CDO=∠ABO=90°,
∴点C的坐标为(2,3),点D的坐标为(2,0);
(2)∵反比例函数y=
| k |
| x |
∴k=2×3=6,
∴反比例函数的解析式为y=
| 6 |
| x |
∵△EFH是由△COD向右平移m(m>0)个单位所得,
∴点E的坐标为(2+m,3),点F的坐标为(m,0).
∴EF的中点M坐标为(
| 2+m+m |
| 2 |
| 3+0 |
| 2 |
| 3 |
| 2 |
∵反比例函数y=
| 6 |
| x |
| 3 |
| 2 |
∴
| 3 |
| 2 |
解得:m=3,
∴m的值为3;
(3)由平移的性质可得:OF=CE,OF∥CE,
∴四边形OFEC是平行四边形,
∴S?OFEC=OF•EH=3×3=9,
即四边形OFEC的面积为9.
点评:本题主要考查了用待定系数法求反比例函数的解析式、旋转的性质、平移的性质、中点坐标公式、平行四边形的面积公式等知识,运用旋转及平移的性质是解决本题的关键.

练习册系列答案
相关题目
下列说法正确的是( )
A、“掷一枚硬币正面朝上的概率是
| ||
| B、一组数据2,2,3,6的众数和中位数都是2 | ||
| C、要了解全市人民的低碳生活状况,适宜采用抽样调查的方法 | ||
| D、随机抽取甲、乙两名同学的5次数学成绩,计算得平均分都是90分,方差分别是S2甲=5,S2乙=12,说明乙的成绩较为稳定 |

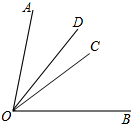 已知:如图,OC平分∠AOB,OD与OC不重合且在∠AOC内部,求证:∠DOC=
已知:如图,OC平分∠AOB,OD与OC不重合且在∠AOC内部,求证:∠DOC=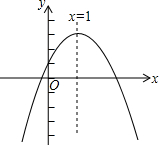 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论: