Question

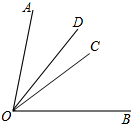已知：如图，OC平分∠AOB，OD与OC不重合且在∠AOC内部，求证：∠DOC=

1

2

（∠BOD-∠AOD）．

Answer 1

考点：角平分线的定义

专题：证明题

分析：先根据角平分线的定义得出OC平分∠AOB，∠BOC=∠AOC=

1

2

∠AOB，再由OD与OC不重合且在∠AOC内部即可得出结论．

解答：证明：∵OC平分∠AOB，
∴∠BOC=∠AOC=

1

2

∠AOB．
∵OD与OC不重合且在∠AOC内部，
∴∠BOD-∠AOD=2∠DOC，
∴∠DOC=

1

2

（∠BOD-∠AOD）．

点评：本题考查的是角平分线的定义，熟知从一个角的顶点出发，把这个角分成相等的两个角的射线叫做这个角的平分线是解答此题的关键．