题目内容
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:
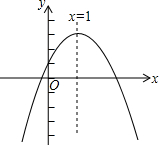
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc<0;②b>a+c;③2a-b=0;④b2-4ac<0.
其中正确的结论个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:二次函数图象与系数的关系
专题:
分析:由抛物线开口方向得到a<0,由抛物线与y轴的交点在x轴上方得到c>0,由于抛物线的对称轴为直线x=-
=1,则b=-2a>0;则abc<0;根据抛物线与x轴有2个交点得到△=b2-4ac>0;由于x=-1时,y>0,于是有a-b+c<0.
| b |
| 2a |
解答:解:∵抛物线开口向下,
∴a<0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
由于抛物线的对称轴为直线x=-
=1,则b=-2a>0;则2a+b>0,abc<0;
∴①正确,
∴③错误;
∵抛物线与x轴有2个交点,
∴△=b2-4ac>0,所以④错误;
∵x=-1时,y<0,
∴a-b+c<0,所以②正确.
故选B.
∴a<0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
由于抛物线的对称轴为直线x=-
| b |
| 2a |
∴①正确,
∴③错误;
∵抛物线与x轴有2个交点,
∴△=b2-4ac>0,所以④错误;
∵x=-1时,y<0,
∴a-b+c<0,所以②正确.
故选B.
点评:本题考查了二次函数图象与系数的关系:二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小,当 a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置,当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定,△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下面四个图形中,∠1和∠2不属于同旁内角的是( )
A、 |
B、 |
C、 |
D、 |
 如图,A、O、E三点在同一直线上,∠DOE=20°,OB平分∠AOC,且∠COD:∠BOC=2:3,求∠AOC的度数.
如图,A、O、E三点在同一直线上,∠DOE=20°,OB平分∠AOC,且∠COD:∠BOC=2:3,求∠AOC的度数. 如图,等边△ABC的顶点A(-2
如图,等边△ABC的顶点A(-2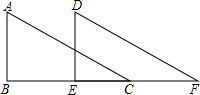 如图,Rt△ABC沿直角边BC所在直线向右平移得到△DEF,下列结论:
如图,Rt△ABC沿直角边BC所在直线向右平移得到△DEF,下列结论: 计算图中阴影部分的面积.
计算图中阴影部分的面积.