题目内容
9.先化简,再求值$\frac{x-4}{x-1}$÷(x+1-$\frac{15}{x-1}$)的值,其中x=8sin30°+2cos45°.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,利用特殊角的三角函数值求出x的值,代入计算即可求出值.
解答 解:原式=$\frac{x-4}{x-1}$÷$\frac{{x}^{2}-1-15}{x-1}$=$\frac{x-4}{x-1}$•$\frac{x-1}{(x+4)(x-4)}$=$\frac{1}{x+4}$,
当x=-8sin30°+2cos45°=-8×$\frac{1}{2}$+2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$-4时,原式=$\frac{\sqrt{2}}{2}$.
点评 此题考查了分式的化简求值,以及特殊角的三角函数值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
19.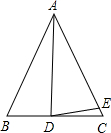 如图,在△ABC中,AB=AC,AD=AE,∠BAD=30°,∠EDC的度数是( )
如图,在△ABC中,AB=AC,AD=AE,∠BAD=30°,∠EDC的度数是( )
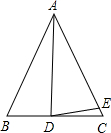 如图,在△ABC中,AB=AC,AD=AE,∠BAD=30°,∠EDC的度数是( )
如图,在△ABC中,AB=AC,AD=AE,∠BAD=30°,∠EDC的度数是( )| A. | 10° | B. | 15° | C. | 20° | D. | 25° |
20.下列命题①过一点有且只有一条直线平行已知直线;②过一点有且只有一条直线与已知直线垂直;③平行同一直线的两条直线互相平行;④平方根等于本身的数是0或1;⑤如果一个数有立方根,那么它一定有平方根,其中假命题的个数为( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
14.若双曲线y=$\frac{k}{x}$上有一点A的坐标为(-2,3),则k的值为( )
| A. | -3 | B. | 6 | C. | 3 | D. | -6 |
1.二次根式$\sqrt{2x+1}$中x的取值范围是( )
| A. | x≥-$\frac{1}{2}$ | B. | x≥$\frac{1}{2}$ | C. | x>$\frac{1}{2}$ | D. | x>-$\frac{1}{2}$ |
10.若α,β是方程x2-2x-2=0的两个实数根,则α2+β2的值为( )
| A. | 10 | B. | 9 | C. | 8 | D. | 7 |
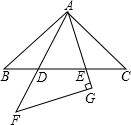 将两块完全相同的等腰直角三角形摆放成如图的样子,假设图形中的所有点、线都在同一平面内,图中有相似(不包括全等)三角形吗?如果有,请写出其中的一对,并给予说明其为什么相似?
将两块完全相同的等腰直角三角形摆放成如图的样子,假设图形中的所有点、线都在同一平面内,图中有相似(不包括全等)三角形吗?如果有,请写出其中的一对,并给予说明其为什么相似?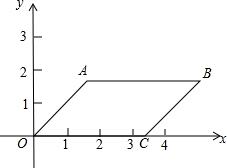 如图,在平行四边形OABC中,已知AB=OC,AB∥OC.A、C两点的坐标分别为$A(\sqrt{3},\sqrt{3}),C(2\sqrt{3},0)$.
如图,在平行四边形OABC中,已知AB=OC,AB∥OC.A、C两点的坐标分别为$A(\sqrt{3},\sqrt{3}),C(2\sqrt{3},0)$.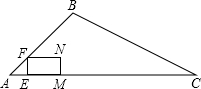 如图,在△ABC中,∠BAC=45°,AB=4$\sqrt{2}$cm,AC=12cm,点E从点A出发沿AC方向以1cm/s的速度运动到点C停止,作EF⊥AC交折线AB-BC于点F,以EF为边向右作矩形EFNM,使EM=2EF.设点E的运动时间为t(s).
如图,在△ABC中,∠BAC=45°,AB=4$\sqrt{2}$cm,AC=12cm,点E从点A出发沿AC方向以1cm/s的速度运动到点C停止,作EF⊥AC交折线AB-BC于点F,以EF为边向右作矩形EFNM,使EM=2EF.设点E的运动时间为t(s).