题目内容
19．
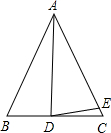如图，在△ABC中，AB=AC，AD=AE，∠BAD=30°，∠EDC的度数是（ ）| A． | 10° | B． | 15° | C． | 20° | D． | 25° |
分析 可以设∠EDC=x，∠B=∠C=y，根据∠ADE=∠AED=x+y，∠ADC=∠B+∠BAD即可列出方程，从而求解．
解答 解：设∠EDC=x，∠B=∠C=y，
∠AED=∠EDC+∠C=x+y，
又因为AD=AE，所以∠ADE=∠AED=x+y，
则∠ADC=∠ADE+∠EDC=2x+y，
又因为∠ADC=∠B+∠BAD，
所以 2x+y=y+30，
解得x=15，
所以∠EDC的度数是15°．
故选B．
点评 本题主要考查了等腰三角形的性质，等边对等角．正确确定相等关系列出方程是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
10．
如图，已知在正方形网格中的两个格点三角形是位似形，它们的位似中心是（ ）
如图，已知在正方形网格中的两个格点三角形是位似形，它们的位似中心是（ ）| A． | 点A | B． | 点B | C． | 点C | D． | 点D |
7．
如图，AB=AC，D、E在BC上且AD=AE，AF⊥BC于点F则图中全等三角形有（ ）
如图，AB=AC，D、E在BC上且AD=AE，AF⊥BC于点F则图中全等三角形有（ ）| A． | 1对 | B． | 2对 | C． | 3对 | D． | 4对 |
14．
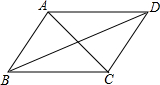如图，下列条件不能够判定AB∥DC的是（ ）
如图，下列条件不能够判定AB∥DC的是（ ）| A． | ∠BAC=∠ACD | B． | ∠DCB+∠ABC=180° | C． | ∠ABD=∠BDC | D． | ∠DAC=∠BCA |
如图，矩形ABCD中，AB=8，BC=6，点E在边AB上，点F在边CD上，点G、H在对角线AC上，若四边形EGFH是菱形，则AE的长是（ ）
11．
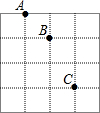如图，利用平面直角坐标系画出的正方形网格中，若A（0，2），B（1，1），则点C的坐标为（ ）
如图，利用平面直角坐标系画出的正方形网格中，若A（0，2），B（1，1），则点C的坐标为（ ）| A． | （1，-2） | B． | （2，1） | C． | （1，-1） | D． | （2，-1） |
8．甲和乙一起做游戏，下列游戏规则对双方公平的是（ ）
| A． | 在一个装有2个红球和3个白球（每个球除颜色外都相同）的袋中任意摸出一球，摸到红球甲获胜，摸到白球乙获胜； | |
| B． | 从标有号数1到100的100张卡片中，随意抽取一张，抽到号数为奇数甲获胜，否则乙获胜； | |
| C． | 任意掷一枚质地均匀的骰子，掷出的点数小于4则甲获胜，掷出的点数大于4则乙获胜； | |
| D． | 让小球在如图所示的地板上自由地滚动，并随机地停在某块方块上，若小球停在黑色区域则甲获胜，若停在白色区域则乙获胜 |