题目内容
8.圆心坐标为(-1,0)的圆与x轴相交于A,B两点,已知A($\sqrt{2}$,0),则点B的坐标为(-2-$\sqrt{2}$,0).分析 设点B坐标为(m,0),圆心O′的坐标为(-1,0),A($\sqrt{2}$,0),根据O′A=O′B,可得方程-1-m=$\sqrt{2}$-(-1),解方程即可解决问题.
解答 解:设点B坐标为(m,0),圆心O′的坐标为(-1,0),
∵A($\sqrt{2}$,0),O′A=O′B,
∴-1-m=$\sqrt{2}$-(-1),
∴m=-2-$\sqrt{2}$,
∴点B坐标为(-2-$\sqrt{2}$,0).
故答案为(-2-$\sqrt{2}$,0).
点评 本题考查坐标与图形的性质,圆的有关知识,解题的关键是学会构建方程解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
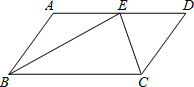 如图,在平行四边形ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=12,CE=5,则平行四边形ABCD的周长是39.
如图,在平行四边形ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=12,CE=5,则平行四边形ABCD的周长是39.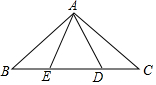 如图,在△ABC中,∠BAC=90°,AB=AC=5,点D,E在BC上,且∠DAE=45°,若CD=$\sqrt{2}$,则DE=$\frac{17\sqrt{2}}{8}$.
如图,在△ABC中,∠BAC=90°,AB=AC=5,点D,E在BC上,且∠DAE=45°,若CD=$\sqrt{2}$,则DE=$\frac{17\sqrt{2}}{8}$.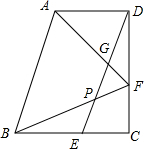 已知:如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=CD,点E、F分别在边BC、CD上,且BE=DF=AD,联结DE,联结AF、BF分别与DE交于点G、P.
已知:如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=CD,点E、F分别在边BC、CD上,且BE=DF=AD,联结DE,联结AF、BF分别与DE交于点G、P.