题目内容
18.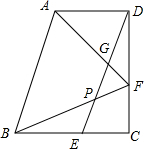 已知:如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=CD,点E、F分别在边BC、CD上,且BE=DF=AD,联结DE,联结AF、BF分别与DE交于点G、P.
已知:如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=CD,点E、F分别在边BC、CD上,且BE=DF=AD,联结DE,联结AF、BF分别与DE交于点G、P.(1)求证:AB=BF;
(2)如果BE=2EC,求证:DG=GE.
分析 (1)先证△BCF≌△DCE,再证四边形ABED是平行四边形,从而得AB=DE=BF.
(2)延长AF交BC延长线于点M,从而CM=CF,又由AD∥BC可以得到$\frac{DG}{GE}$=$\frac{AD}{EM}$=1,从而DG=GE.
解答 证明:(1)∵BC=CD,BE=DF,
∴CF=CE,
在△BCF与△DCE中,
$\left\{\begin{array}{l}{CF=CE}\\{∠C=∠C=90°}\\{BC=DC}\end{array}\right.$,
∴△BCF≌△DCE,
∴BF=DE,
∵AD∥BC,BE=AD,
∴四边形ABED是平行四边形; ∴AB=DE,
∴AB=DE,
∴AB=BF.
(2)延长AF交BC延长线于点M,则CM=CF;
∵AD∥BC,
∴$\frac{DG}{GE}$=$\frac{AD}{EM}$,
∵BE=2EC,
∴$\frac{DG}{GE}$=$\frac{AD}{EM}$=1,
∴DG=GE.
点评 此题主要考查了平行四边形的判定与性质以及全等三角形的判定与性质等知识,根据已知得出△BCF≌△DCE是解题关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
9.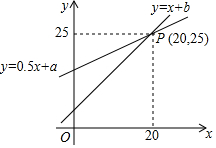 如图,一次函数y=x+b与y=0.5x+a图象交点为P(20,25).则不等式:x+b>0.5x+a的解集是( )
如图,一次函数y=x+b与y=0.5x+a图象交点为P(20,25).则不等式:x+b>0.5x+a的解集是( )
 如图,一次函数y=x+b与y=0.5x+a图象交点为P(20,25).则不等式:x+b>0.5x+a的解集是( )
如图,一次函数y=x+b与y=0.5x+a图象交点为P(20,25).则不等式:x+b>0.5x+a的解集是( )| A. | x>25 | B. | x>20 | C. | x<25 | D. | x<20 |
 如图,将三角形ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的三角形A1B1C1.
如图,将三角形ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的三角形A1B1C1.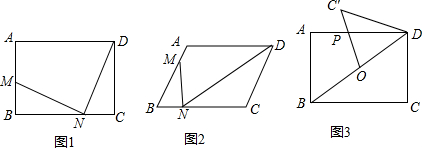
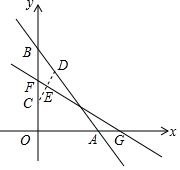 如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别相交于点A,B,点C从点O出发沿射线OB方向以每秒1个单位速度运动,同时点D从点B出发沿BA方向以相同的速度向点A运动.当点D到达点A同时停止运动,点C也随之停止.连接CD,过CD的中点E作EF⊥CD交y轴于点F,交x轴于点G,设运动的时间时t秒.
如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别相交于点A,B,点C从点O出发沿射线OB方向以每秒1个单位速度运动,同时点D从点B出发沿BA方向以相同的速度向点A运动.当点D到达点A同时停止运动,点C也随之停止.连接CD,过CD的中点E作EF⊥CD交y轴于点F,交x轴于点G,设运动的时间时t秒. 如图,经过点A(0,6)的抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于B(-2,0)、C两点.
如图,经过点A(0,6)的抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于B(-2,0)、C两点.