题目内容
8.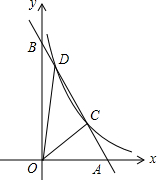 如图,已知直线y1=ax+b与x轴、y轴分别交于A、B两点,与双曲线y2=$\frac{k}{x}$(x>0)交于C(m,n)、D(p,q)两点,连接OC、OD.
如图,已知直线y1=ax+b与x轴、y轴分别交于A、B两点,与双曲线y2=$\frac{k}{x}$(x>0)交于C(m,n)、D(p,q)两点,连接OC、OD.(1)若C、D两点的坐标分别为C(3,1)、D($\frac{1}{2}$,6),利用图象求:当y1<y2时,x的取值范围;
(2)若k=2,设△OCD的面积为S,求证:S=$\frac{m}{p}$-$\frac{p}{m}$.
分析 (1)直接根据两函数图象的交点即可得出结论;
(2)由k=2,得到y2=$\frac{2}{x}$,于是得到n=$\frac{2}{m}$,q=$\frac{2}{p}$,过D作DE⊥OA于D,过C作CF⊥OA与F,根据△OCD的面积=四边形CDEF的面积,列方程即可得到结论.
解答  解:(1)由函数图象可知,当y1<y2时,x的取值范围是:0<x<$\frac{1}{2}$或x>1;
解:(1)由函数图象可知,当y1<y2时,x的取值范围是:0<x<$\frac{1}{2}$或x>1;
(2)∵k=2,
∴y2=$\frac{2}{x}$,
∴n=$\frac{2}{m}$,q=$\frac{2}{p}$,
过D作DE⊥OA于D,过C作CF⊥OA与F,
∵S△DOE=S△COF,
∴△OCD的面积=四边形CDEF的面积,
∴S=$\frac{1}{2}$($\frac{2}{m}$+$\frac{2}{p}$)(m-p)=$\frac{m}{p}$-$\frac{p}{m}$.
点评 本题考查的是反比例函数与一次函数的交点问题、图形的面积的计算,根据题意作出辅助线是解答此题的关键.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 中考英语听力测试期间T需要杜绝考点周围的噪音.如图,点A是某市一中考考点,在位于考点南偏西15°方向距离500米的C点处有一消防队.在听力考试期间,消防队突然接到报警电话,消防车需沿北偏东75°方向的公路CF前往救援.已知消防车的警报声传播半径为400米,若消防车的警报声对听力测试造成影响,则消防车必须改道行驶.试问:消防车是否需要改道行驶?
中考英语听力测试期间T需要杜绝考点周围的噪音.如图,点A是某市一中考考点,在位于考点南偏西15°方向距离500米的C点处有一消防队.在听力考试期间,消防队突然接到报警电话,消防车需沿北偏东75°方向的公路CF前往救援.已知消防车的警报声传播半径为400米,若消防车的警报声对听力测试造成影响,则消防车必须改道行驶.试问:消防车是否需要改道行驶?


 如图1,AB是⊙O的直径,BC是⊙O的切线,OC∥弦AD,连接BD交AC于E.
如图1,AB是⊙O的直径,BC是⊙O的切线,OC∥弦AD,连接BD交AC于E.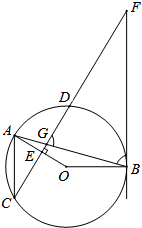 如图,在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B的直线与CD的延长线交于点F,AC∥BF.
如图,在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B的直线与CD的延长线交于点F,AC∥BF.