��Ŀ����
9����֪����ͼ�٣���Rt��ABC�У�AB��AC��AB=3cm��BC=5cm������ABC��AC�е���ת180��á�CDA����ͼ�ڣ��ٽ���CDA��AC�ķ�����1cm/s���ٶ�ƽ�Ƶõ���NDP��ͬʱ����Q�ӵ�C��������CB������1cm/s���ٶ��˶�������NDPֹͣƽ��ʱ����QҲֹͣ�˶������˶�ʱ��Ϊt��s����0��t��4��������������⣮
��1����tΪ��ֵʱ��PQ��AB��
��2�����PQC�����Ϊy��cm2������y��t֮��ĺ�����ϵʽ��
��3���Ƿ����ijһʱ��t��ʹS��QDC��S�ı���ABQP=1��4�������ڣ����t��ֵ���������ڣ���˵�����ɣ�
��4���Ƿ����ijһʱ��t��ʹPQ��DQ�������ڣ���ֱ��д��t��ֵ���������ڣ���˵�����ɣ�
���� ��1���ȸ��ݹ��ɶ�����AC=4������ƽ�Ƶ����ʺ�ƽ���ı��ε����ʵã�PQ��AB���б���ʽΪ$\frac{CP}{CA}$=$\frac{CQ}{CB}$���������t��ֵ��
��2���������ߣ��������ߣ������������AE�ij������ù��ɶ�������CE�ij���֤����CPF�ס�CAE����ʽ�ɱ�ʾPF�ij������������ʽ����y��t֮��ĺ�����ϵʽ��
��3������ͬ�ȸߵ����������������ȵã�S��PQC=S��MQC������֪�ã�S��MQC��S��ABC=1��5���ѣ�2���е�ʽ�Ӵ������t��ֵ��
��4����ͼ2��֤����MQP�ס�PFQ���б���ʽ����ã�PQ2=PM��FQ���ɹ��ɶ������ϵã�PF2+FQ2=PM��FQ�������з��̿ɵý��ۣ�
��� �⣺��1����Rt��ABC�У��ɹ��ɶ����ã�
AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=4��
��ƽ�����ʿɵ�MN��AB��
��PQ��MN��
��PQ��AB��
��$\frac{CP}{CA}$=$\frac{CQ}{CB}$����$\frac{4-t}{4}$=$\frac{t}{5}$��
��ã�t=$\frac{20}{9}$��
��2����ͼ2����PF��BC�ڵ�F��AE��BC�ڵ�E��
��S��ABC=$\frac{1}{2}$AB��AC=$\frac{1}{2}$AE��BC�ɵã�$\frac{1}{2}$��3��4=$\frac{1}{2}$��5AE��
��AE=$\frac{12}{5}$��
�ɹ��ɶ����ã�CE=$\sqrt{A{C}^{2}-A{E}^{2}}$=$\frac{16}{5}$��
��PF��BC��AE��BC��
��AE��PF��
���CPF�ס�CAE��
��$\frac{CP}{CA}$=$\frac{CF}{CE}$=$\frac{PF}{AE}$����$\frac{4-t}{4}$=$\frac{CF}{\frac{16}{5}}$=$\frac{PF}{\frac{12}{5}}$��
��ã�CF=$\frac{16-4t}{5}$��PF=$\frac{12-3t}{5}$��
��PM��BC������M��BC�ľ���h=PF=$\frac{12-3t}{5}$��
���QCM�����y=$\frac{1}{2}$CQ��h=$\frac{1}{2}$��t��$\frac{12-3t}{5}$=-$\frac{3}{10}$t2+6t��
��3����PM��BC��
��S��PQC=S��MQC��
��S��QMC��S�ı���ABQP=1��4��
��S��MQC��S��ABC=1��5��
��5��-$\frac{3}{10}$t2+6t��=$\frac{1}{2}$��4��3��
t2-4t+4=0��
��ã�t1=t2=2��
�൱t=2ʱ��S��QMC��S�ı���ABQP=1��4��
��4����ͼ2����PQ��MQ��
���MQP=��PFQ=90�㣬
��MP��BC��
���MPQ=��PQF��
���MQP�ס�PFQ��
��$\frac{PM}{PQ}$=$\frac{PQ}{FQ}$��
��PQ2=PM��FQ��
��PF2+FQ2=PM��FQ��
��CF=$\frac{16-4t}{5}$����FQ=CF-CQ=$\frac{16-9t}{5}$��
��$\frac{12-3t}{5}$��2+��$\frac{16-9t}{5}$��2=5��$\frac{16-9t}{5}$��
������2t2-3t=0��
���t1=0���ᣩ��t2=$\frac{3}{2}$��
�𣺵�t=$\frac{3}{2}$ʱ��PQ��MQ��
���� �������ı��ε��ۺ��⣬������ƽ���ı��Ρ�ƽ�ơ����ɶ��������������ε����ʺ��ж�������ƽ�Ƶ��ص㣬ȷ��������ϵ�ǹؼ����������������е�����ϵ��Ҳ����������֪����ı��е�����ϵ���ⷽ�̿��Խ�����⣮

 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�| A�� | 1 | B�� | $\sqrt{2}$ | C�� | $\sqrt{3}$ | D�� | $\sqrt{5}$ |
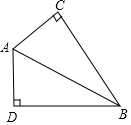 ��ͼ����C=��D=90�㣬AC=AD����ô��ABC���ABDȫ�ȵ������ǣ�������
��ͼ����C=��D=90�㣬AC=AD����ô��ABC���ABDȫ�ȵ������ǣ�������| A�� | HL | B�� | SAS | C�� | ASA | D�� | AAS |
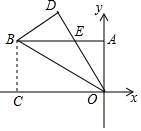 ������OABC��ƽ��ֱ������ϵ�ڵ�λ����ͼ��ʾ������������BO�۵���ʹ��C���ڵ�D����DO��AB���ڵ�E��BC=4cm��BA=8cm�����E������Ϊ��������
������OABC��ƽ��ֱ������ϵ�ڵ�λ����ͼ��ʾ������������BO�۵���ʹ��C���ڵ�D����DO��AB���ڵ�E��BC=4cm��BA=8cm�����E������Ϊ��������| A�� | ��-3��4�� | B�� | ��-3.5��4�� | C�� | ��-3.7��4�� | D�� | ��-4��4�� |
| A�� | -5-��+5��=-10 | B�� | -3+2=-1 | C�� | ��-3������+5��=-15 | D�� | |-2|+��-4��=2 |
 ��ͼ��������ABCD�Ķ���A������Ϊ��0��3��������B������������ϣ�tan��OBA=3���Խ���AC��BD���ڵ�P������OP��AB�ڵ�N����DC�ڵ�M����R��O������OM������ÿ��$\sqrt{2}$����λ���ٶ��˶����˶�ʱ��Ϊt��
��ͼ��������ABCD�Ķ���A������Ϊ��0��3��������B������������ϣ�tan��OBA=3���Խ���AC��BD���ڵ�P������OP��AB�ڵ�N����DC�ڵ�M����R��O������OM������ÿ��$\sqrt{2}$����λ���ٶ��˶����˶�ʱ��Ϊt��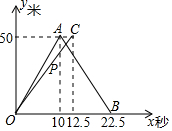 �ס�����������������ֱ�ܵ��Ͻ��о��߱�����ע���ܵ���50�ף����˾�����һ�Σ�����ʱת����ʱ����Բ��ƣ���ͼ�е�����OA-AB�Ǽ��������ľ���y���ף������ʱ��x���룩�ĺ���ͼ���߶�OC�����������ľ���y���ף������ʱ��x���룩�ĺ���ͼ������x��0���߶�OC��AB�ཻ�ڵ�P������ͼ����������⣺
�ס�����������������ֱ�ܵ��Ͻ��о��߱�����ע���ܵ���50�ף����˾�����һ�Σ�����ʱת����ʱ����Բ��ƣ���ͼ�е�����OA-AB�Ǽ��������ľ���y���ף������ʱ��x���룩�ĺ���ͼ���߶�OC�����������ľ���y���ף������ʱ��x���룩�ĺ���ͼ������x��0���߶�OC��AB�ཻ�ڵ�P������ͼ����������⣺