题目内容
19.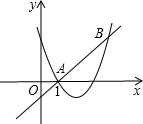 如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B,且当x=4时,二次函数的值为6.
如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B,且当x=4时,二次函数的值为6.(1)求m的值和抛物线的解析式;
(2)求不等式x2+bx+c>x+m的解集.
分析 (1)直接把点A(1,0)代入直线y=x+m即可得出m的值;再把点A(1,0)与当x=4时,y=6代入抛物线y=x2+bx+c即可得出b、c的值,进而得出抛物线的解析式;
(2)根据(1)中m、b、c的值即可得出一次函数与二次函数的解析式,故可得出B点坐标,根据函数的图象即可得出结论.
解答 解:(1)∵直线y=x+m和经过点A(1,0),
∴1+m=0,解得m=-1;
∵抛物线y=x2+bx+c经过点A(1,0),且当x=4时,二次函数的值为6,
∴$\left\{\begin{array}{l}1+b+c=0\\ 16+4b+c=6\end{array}\right.$,解得$\left\{\begin{array}{l}b=-3\\ c=2\end{array}\right.$,
∴抛物线的解析式为y=x2-3x+2;
(2)∵由(1)知m=-1,抛物线的解析式为y=x2-3x+2,
∴直线的解析式为y=x-1,
∴$\left\{\begin{array}{l}y=x-1\\ y={x}^{2}-3x+2\end{array}\right.$,解得$\left\{\begin{array}{l}x=3\\ y=2\end{array}\right.$或$\left\{\begin{array}{l}x=1\\ y=0\end{array}\right.$,
∴B(3,2).
∵由函数图象可知,当x<1或x>3时,二次函数的值大于一次函数的值,
∴不等式x2+bx+c>x+m的解集为x<1或x>3.
点评 本题考查的是二次函数与不等式,能根据题意利用数形结合求出不等式的解集是解答此题的关键.

练习册系列答案
相关题目
9.设a,b是实数,且$\frac{1}{1+a}-\frac{1}{1+b}=\frac{1}{b-a}$,则$\frac{1+b}{1+a}-\frac{1+a}{1+b}$的值是( )
| A. | 3 | B. | -3 | C. | 3(b-a) | D. | 无法确定 |
4.下列二次函数的图象与x轴有两个交点的是( )
| A. | y=-x2-6x+9 | B. | y=2x2-x+1 | C. | y=-x2+2x-5 | D. | y=2x2-4x+1 |
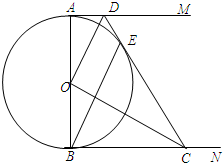 如图,AB是⊙O的直径,AM和BN是它的两条切线,DE切⊙O于点E,交AM于点D,交BN于点C,
如图,AB是⊙O的直径,AM和BN是它的两条切线,DE切⊙O于点E,交AM于点D,交BN于点C, 如图,⊙O直径AB与弦CD相交于E,∠AED=60°,AE=3,BE=7,求CD长.
如图,⊙O直径AB与弦CD相交于E,∠AED=60°,AE=3,BE=7,求CD长.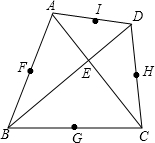 已知:如图,四边形ABCD的对角线AC⊥BD,垂足为E,点F,G,H,I分别是四边形各边中点.求证:F,G,H,I四个点在同一个圆上.
已知:如图,四边形ABCD的对角线AC⊥BD,垂足为E,点F,G,H,I分别是四边形各边中点.求证:F,G,H,I四个点在同一个圆上.