题目内容
4.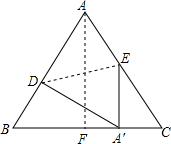 如图,△ABC是正三角形,点E是AC边上的中点,将三角形的一部分沿着DE折叠,使得点A于BC边上的某一点A′重合,若∠BEA′-∠A′EC=∠BAC,求∠ADE.
如图,△ABC是正三角形,点E是AC边上的中点,将三角形的一部分沿着DE折叠,使得点A于BC边上的某一点A′重合,若∠BEA′-∠A′EC=∠BAC,求∠ADE.
分析 根据等腰三角形的三线合一得到∠BEC=90°,根据题意求出∠BEA′和∠A′EC的度数,根据翻折变换的性质和三角形内角和定理计算即可.
解答 解: △ABC是正三角形,点E是AC边上的中点,
△ABC是正三角形,点E是AC边上的中点,
∴∠BEC=90°,即∠BEA′+∠A′EC═90°,
又∵∠BEA′-∠A′EC=∠BAC=60°,
解得∠BEA′=75°,∠A′EC=15°,
∴∠AED=$\frac{1}{2}$(180°-15°)=82.5°,
∴∠ADE=180°-60°-82.5°=37.5°.
点评 本题考查的是翻折变换的性质、三角形内角和定理的应用,找准翻折变换中的对应角和对应边是解题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
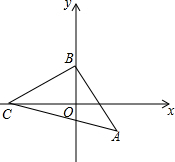 如图,已知B(0,1),C(-2,0),过点B作AB⊥BC,使得AB=BC.
如图,已知B(0,1),C(-2,0),过点B作AB⊥BC,使得AB=BC. 如图,已知△ABC,AD是∠BAC的平分线,AE是∠BAC的外角∠FAC的平分线.
如图,已知△ABC,AD是∠BAC的平分线,AE是∠BAC的外角∠FAC的平分线. 已知,如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过O作OE∥AB交BC于E.
已知,如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过O作OE∥AB交BC于E.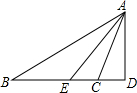 如图,△ABC中,∠B=36°,∠ACB=110°,AE是∠BAC的平分线,AD是BC边上的高,求∠DAE的大小.
如图,△ABC中,∠B=36°,∠ACB=110°,AE是∠BAC的平分线,AD是BC边上的高,求∠DAE的大小. 如图,⊙O直径AB与弦CD相交于E,∠AED=60°,AE=3,BE=7,求CD长.
如图,⊙O直径AB与弦CD相交于E,∠AED=60°,AE=3,BE=7,求CD长.