题目内容
8.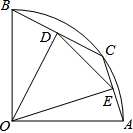 如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点,OD⊥BC,OE⊥AC,垂足分别为D、E.设BD=m,则m的取值范围是0<m<$\sqrt{2}$,.
如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点,OD⊥BC,OE⊥AC,垂足分别为D、E.设BD=m,则m的取值范围是0<m<$\sqrt{2}$,.
分析 连接AB,由OD垂直于BC,OE垂直于AC,利用垂径定理得到D、E分别为BC、AC的中点,即ED为三角形ABC的中位线,由OA=OB=2,且∠AOB=90°,利用勾股定理求出AB的长,即可求出DE的长.
解答 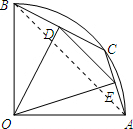 解:连接AB,
解:连接AB,
∵OD⊥BC,
∴D、为BC的中点,
∴BC=2BD=2m,
∵OA=OB=2,∠AOB=90°,
∴根据勾股定理得:AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=2$\sqrt{2}$,
∵点C是弧AB上的一个动点,
∴0<BC<AB,
即0<2m<2$\sqrt{2}$,
∴0<m<$\sqrt{2}$,
故答案为:0<m<$\sqrt{2}$.
点评 此题考查了垂径定理,勾股定理,以及三角形的中位线定理,熟练掌握定理是解本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
16.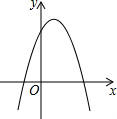 已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c+2=0的根的情况是( )
已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c+2=0的根的情况是( )
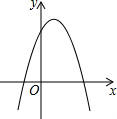 已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c+2=0的根的情况是( )
已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c+2=0的根的情况是( )| A. | 无实数根 | B. | 有两个同号不等实数根 | ||
| C. | 有两个异号实数根 | D. | 有两个相等实数根 |
13.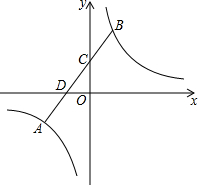 如图,点A、B分别在反比例函数y=$\frac{k}{x}$图象的两支上,连接AB交x轴于点C,交y轴于点D,则AD与BC的大小关系为( )
如图,点A、B分别在反比例函数y=$\frac{k}{x}$图象的两支上,连接AB交x轴于点C,交y轴于点D,则AD与BC的大小关系为( )
 如图,点A、B分别在反比例函数y=$\frac{k}{x}$图象的两支上,连接AB交x轴于点C,交y轴于点D,则AD与BC的大小关系为( )
如图,点A、B分别在反比例函数y=$\frac{k}{x}$图象的两支上,连接AB交x轴于点C,交y轴于点D,则AD与BC的大小关系为( )| A. | AD>BC | B. | AD=BC | C. | AD<BC | D. | 无法判断 |
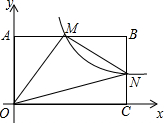 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在坐标轴上,点B的坐标为(4,2),直线y=-$\frac{1}{2}$x+3交AB,BC于点M,N,反比例函数y=$\frac{k}{x}$的图象经过点M,N.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在坐标轴上,点B的坐标为(4,2),直线y=-$\frac{1}{2}$x+3交AB,BC于点M,N,反比例函数y=$\frac{k}{x}$的图象经过点M,N. 在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2012个正方形的面积为5•($\frac{3}{2}$)4022.
在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2012个正方形的面积为5•($\frac{3}{2}$)4022.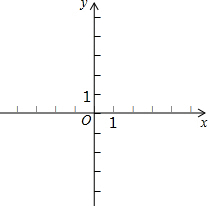 (1)在所给平面直角坐标系中,画出反比例函数y=$\frac{4}{x}$的图象;
(1)在所给平面直角坐标系中,画出反比例函数y=$\frac{4}{x}$的图象;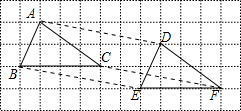 经过平移,△ABC移到△DEF的位置,如图,下列结论:①AD=BE=CF,且AD∥BE∥CF;②AB∥DE,BC∥EF,BC=EF;③AB=DE,BC=EF,AC=DF.正确的有( )
经过平移,△ABC移到△DEF的位置,如图,下列结论:①AD=BE=CF,且AD∥BE∥CF;②AB∥DE,BC∥EF,BC=EF;③AB=DE,BC=EF,AC=DF.正确的有( )