题目内容
16．
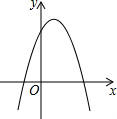已知函数y=ax2+bx+c的图象如图所示，那么关于x的方程ax2+bx+c+2=0的根的情况是（ ）| A． | 无实数根 | B． | 有两个同号不等实数根 | ||
| C． | 有两个异号实数根 | D． | 有两个相等实数根 |
分析 由图象可知a，b，c的取值范围，利用根的判别式和根与系数的关系可得根的情况．
解答 解：由图象可知a＜0，b＞0，c＞0，b2-4ac＞0，
∴关于x的方程ax2+bx+c+2=0的根的判别式为：△=b2-4a（c+2）=b2-4ac-8a，
∵a＜0，∴-8a＞0，
∵b2-4ac＞0，
∴△＞0，
∴方程有两个不相等的实数根，
又∵两根之和为$-\frac{a}{b}$＞0，两根之积为$\frac{c+2}{a}$＜0，
∴两根异号，
故选C．
点评 本题主要考查了抛物线与x轴的交点和一元二次方程之间的关系，利用根的判别式和根与系数的关系是解答此题的关键．
练习册系列答案
相关题目
4．
如图，正五边形ABCDE，B′是边BC上任意一点，以AB′为边（在BC的上方），向外作正五边形A′B′C′D′E′，连结CC′，则∠B′CC′=（ ）
如图，正五边形ABCDE，B′是边BC上任意一点，以AB′为边（在BC的上方），向外作正五边形A′B′C′D′E′，连结CC′，则∠B′CC′=（ ）| A． | 108° | B． | 126° | C． | 144° | D． | 162° |
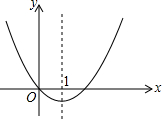二次函数的图象如图，对称轴为x=1．若关于x的一元二次方程x2+bx-t=0（为实数）在-1＜x＜4的范围内有解，则t的取值范围是-1≤t＜8．
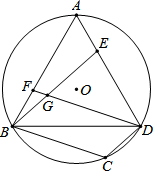如图，已知△ABD为⊙O的内接正三角形，AB=2$\sqrt{7}$，E、F分别为边AD、AB上的动点，且AE=BF，DF与BE相交于G点，过B点作BC∥DF交$\widehat{BD}$于点C，连接CD．
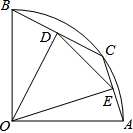如图，在半径为2的扇形AOB中，∠AOB=90°，点C是弧AB上的一个动点，OD⊥BC，OE⊥AC，垂足分别为D、E．设BD=m，则m的取值范围是0＜m＜$\sqrt{2}$，．
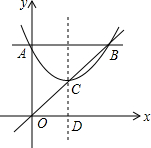如图，抛物线y=$\frac{1}{3}$x2+bx+6与y轴相交于点A，与过点A且平行于x轴的直线相交于点B（点B在第一象限），抛物线的顶点C在直线OB上，平移直线OB，使平移后的直线OB与抛物线只有一个交点，则直线OB向右平移了$\frac{3}{4}$个单位．