题目内容
18.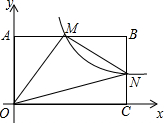 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在坐标轴上,点B的坐标为(4,2),直线y=-$\frac{1}{2}$x+3交AB,BC于点M,N,反比例函数y=$\frac{k}{x}$的图象经过点M,N.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在坐标轴上,点B的坐标为(4,2),直线y=-$\frac{1}{2}$x+3交AB,BC于点M,N,反比例函数y=$\frac{k}{x}$的图象经过点M,N.(1)求反比例函数的解析式;
(2)若点P在x轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
分析 (1)求出OA=BC=2,将y=2代入y=-$\frac{1}{2}$x+3求出x=2,得出M的坐标,把M的坐标代入反比例函数的解析式即可求出答案;
(2)求出四边形BMON的面积,求出OP的值,即可求出P的坐标.
解答 解:(1)∵B(4,2),四边形OABC是矩形,
∴OA=BC=2,
将y=2代入y=-$\frac{1}{2}$x+3得:x=2,
∴M(2,2),
把M的坐标代入y=$\frac{k}{x}$得:k=4,
∴反比例函数的解析式是y=$\frac{4}{x}$;
 (2)把x=4代入y=$\frac{4}{x}$得:y=1,即CN=1,
(2)把x=4代入y=$\frac{4}{x}$得:y=1,即CN=1,
∵S四边形BMON=S矩形OABC-S△AOM-S△CON
=4×2-$\frac{1}{2}$×2×2-$\frac{1}{2}$×4×1=4,
由题意得:$\frac{1}{2}$|OP|×AO=4,
∵AO=2,
∴|OP|=4,
∴点P的坐标是(4,0)或(-4,0).
点评 本题考查了用待定系数法求反比例函数的解析式,一次函数与反比例函数的交点问题,三角形的面积,矩形的性质等知识点的应用,主要考查学生应用性质进行计算的能力,题目比较好,难度适中

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
13.下面是一家商店四年盈亏情况统计表:(单位:万元)
补全该表,并进一步诊断一下,该商店这四年盈利还是亏损?
| 年 | 上半年盈利 | 下半年盈利 | 算式 | 合计 |
| 第一年 | 1.2 | 0.8 | 1.2+0.8 | |
| 第二年 | -0.6 | -0.7 | (-0.6)+(-0.7) | |
| 第三年 | -0.5 | 0.5 | (-0.5)+0.5 | |
| 第四年 | 0.9 | -0.1 | 0.9+(-0.1) |
4. 如图,正五边形ABCDE,B′是边BC上任意一点,以AB′为边(在BC的上方),向外作正五边形A′B′C′D′E′,连结CC′,则∠B′CC′=( )
如图,正五边形ABCDE,B′是边BC上任意一点,以AB′为边(在BC的上方),向外作正五边形A′B′C′D′E′,连结CC′,则∠B′CC′=( )
 如图,正五边形ABCDE,B′是边BC上任意一点,以AB′为边(在BC的上方),向外作正五边形A′B′C′D′E′,连结CC′,则∠B′CC′=( )
如图,正五边形ABCDE,B′是边BC上任意一点,以AB′为边(在BC的上方),向外作正五边形A′B′C′D′E′,连结CC′,则∠B′CC′=( )| A. | 108° | B. | 126° | C. | 144° | D. | 162° |
9.下列运算正确的是( )
| A. | $\sqrt{4}=±2$ | B. | (-3)3=27 | C. | $\sqrt{4}$=2 | D. | $\root{3}{9}$=3 |
 图象中所反映的过程是:小强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示小强离家的距离.图象提供的信息,有以下四个说法:
图象中所反映的过程是:小强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示小强离家的距离.图象提供的信息,有以下四个说法: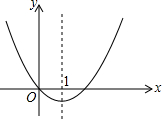 二次函数的图象如图,对称轴为x=1.若关于x的一元二次方程x2+bx-t=0(为实数)在-1<x<4的范围内有解,则t的取值范围是-1≤t<8.
二次函数的图象如图,对称轴为x=1.若关于x的一元二次方程x2+bx-t=0(为实数)在-1<x<4的范围内有解,则t的取值范围是-1≤t<8.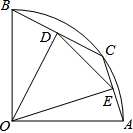 如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点,OD⊥BC,OE⊥AC,垂足分别为D、E.设BD=m,则m的取值范围是0<m<$\sqrt{2}$,.
如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点,OD⊥BC,OE⊥AC,垂足分别为D、E.设BD=m,则m的取值范围是0<m<$\sqrt{2}$,.