题目内容
16.归纳:(一)在数轴上,点A表示数-3,点O表示原点,求点A、O之间的距离;
解:根据绝对值的定义:一个数所对应的点与原点的距离叫做这个数的绝对值,可知点A、O之间的距离为|-3|=3;
(二)在数轴上,点A、B分别表示数a、b,分别计算下列情况中点A、B之间的距离;
(1)当a=2,b=5时,AB=3;
(2)当a=0,b=5时,AB=5;
(3)当a=2,b=-5时,AB=7;
(4)当a=-2,b=-5时,AB=3;
(5)当a=2,b=m时,AB=|m-2|;
总结:
(6)点A、B分别表示数a、b,点A、B之间的距离为|a-b|;
应用:
(7)数轴上分别表示a和-2的两点A和B之间的距离为3,那么a=1或-5;
(8)计算:
|$\frac{1}{3}$-$\frac{1}{2}$|+|$\frac{1}{4}$-$\frac{1}{3}$|+|$\frac{1}{5}$-$\frac{1}{4}$|+L+|$\frac{1}{19}$-$\frac{1}{18}$|+|$\frac{1}{20}$-$\frac{1}{19}$|=$\frac{9}{20}$;
(9)|3-a|+|a-2|的最小值是1.
分析 直接利用(一)的结论和绝对值的定义计算即可.
解答 解:(1)|5-2|=3;
(2)|5-0|=5;
(3)|-5-2|=7;
(4)|-5+2|=3;
(5)|m-2|;
(6)|a-b|;
(7)|a+2|=3;
a+2=±3,
∴a=1或-5;
(8)原式=$\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}$…$+\frac{1}{18}$$-\frac{1}{19}$$+\frac{1}{19}$$-\frac{1}{20}$=$\frac{1}{2}-\frac{1}{20}$=$\frac{9}{20}$;
(9)当2≤a≤3时,|a-2|+|3-a|有最小值.
此时|a-2|=a-2,|3-a|=3-a,
∴|3-a|+|a-2|=3-a+a-2=1.
故答案为:3;5;7;3;|m-2|;|a-b|;-1或5;$\frac{9}{20}$;1.
点评 本题主要考查了绝对值和数轴的定义,理解定义是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.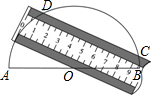 如图,将一个一边有刻度的直尺放在一个量角器上,使其一边经过量角器的圆心O另一边与量角器交于C、D两点,且C、D两点在直尺上的刻度分别为2、10在量角器上的刻度分别为50、170,则直尺的宽为( )
如图,将一个一边有刻度的直尺放在一个量角器上,使其一边经过量角器的圆心O另一边与量角器交于C、D两点,且C、D两点在直尺上的刻度分别为2、10在量角器上的刻度分别为50、170,则直尺的宽为( )
 如图,将一个一边有刻度的直尺放在一个量角器上,使其一边经过量角器的圆心O另一边与量角器交于C、D两点,且C、D两点在直尺上的刻度分别为2、10在量角器上的刻度分别为50、170,则直尺的宽为( )
如图,将一个一边有刻度的直尺放在一个量角器上,使其一边经过量角器的圆心O另一边与量角器交于C、D两点,且C、D两点在直尺上的刻度分别为2、10在量角器上的刻度分别为50、170,则直尺的宽为( )| A. | 2 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
6.若点(m,n)在函数y=2x-1的图象上,则2m-n的值是( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
 如图在△ABC和△DEF中,∠B=50°,∠A=41°,∠E=50°,∠F=89°,求证:△ABC∽△DEF.
如图在△ABC和△DEF中,∠B=50°,∠A=41°,∠E=50°,∠F=89°,求证:△ABC∽△DEF. 小颖想测量教学楼前的一棵树AB的高度,课外活动时她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,如图:她先测得留在墙壁上的影高CD为1.2m,又测得地面的影长BD为2.4m,请你帮她算一下,树高是多少?
小颖想测量教学楼前的一棵树AB的高度,课外活动时她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,如图:她先测得留在墙壁上的影高CD为1.2m,又测得地面的影长BD为2.4m,请你帮她算一下,树高是多少?