题目内容
2. 如图,你能否判断∠1+∠2与∠B+∠C的大小关系?并说明理由.
如图,你能否判断∠1+∠2与∠B+∠C的大小关系?并说明理由.
分析 首先根据邻补角定义得出∠1=180°-∠BAD,∠2=180°-∠ADC,那么∠1+∠2=360°-∠BAD-∠ADC,再由四边形ABCD内角和为360°,得出∠B+∠C=360°-∠BAD-∠ADC,根据等式的性质得出∠1+∠2=∠B+∠C.
解答 解:∠1+∠2=∠B+∠C.理由如下:
∵∠1=180°-∠BAD,∠2=180°-∠ADC,
∴∠1+∠2=180°-∠BAD+180°-∠ADC=360°-∠BAD-∠ADC,
又∵四边形ABCD内角和为360°,
∴∠B+∠C=360°-∠BAD-∠ADC,
∴∠1+∠2=∠B+∠C.
点评 本题考查了多边形内角与外角,多边形内角和定理,掌握多边形的内角与其相邻的外角互为邻补角是解题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
17.下列各式成立的是( )
| A. | $\sqrt{(-3)^{2}}$=-3 | B. | $\sqrt{4+9}$=$\sqrt{4}$+$\sqrt{9}$ | C. | $\sqrt{3×9}$=$\sqrt{3}$×$\sqrt{9}$ | D. | $\sqrt{{x}^{2}}$=x |
12. 有一篮球与铅球如图放置,其俯视图为( )
有一篮球与铅球如图放置,其俯视图为( )
 有一篮球与铅球如图放置,其俯视图为( )
有一篮球与铅球如图放置,其俯视图为( )| A. |  | B. |  | C. |  | D. |  |
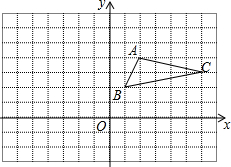 △ABC在平面直角坐标系中的位置如图所示.
△ABC在平面直角坐标系中的位置如图所示.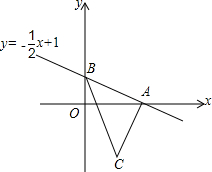 如图,已知直线y=-$\frac{1}{2}$x+1与坐标轴交于A、B两点,C(1,-2),点P在y轴的负半轴上,且S△PAB=S△ABC.
如图,已知直线y=-$\frac{1}{2}$x+1与坐标轴交于A、B两点,C(1,-2),点P在y轴的负半轴上,且S△PAB=S△ABC.
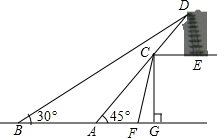 如图为某风景区中古塔,大坝和湖的截面图,大坝顶端CE和水面平行,点C为大坝顶端拐角处,大坝的坡比i=3:1(即CG:FG=3:1),当小明和同伴从大坝的点F处沿着截面所在方向开始划船,划行20米到达点A处时,他们以仰角45°观察远方,正好看到古塔顶端的点D,且点C在视线AD上,当他们从点A继续沿原方向划船40米,到达点B处时,观察点D的仰角正好为30°.
如图为某风景区中古塔,大坝和湖的截面图,大坝顶端CE和水面平行,点C为大坝顶端拐角处,大坝的坡比i=3:1(即CG:FG=3:1),当小明和同伴从大坝的点F处沿着截面所在方向开始划船,划行20米到达点A处时,他们以仰角45°观察远方,正好看到古塔顶端的点D,且点C在视线AD上,当他们从点A继续沿原方向划船40米,到达点B处时,观察点D的仰角正好为30°.