题目内容
13.解下列一元二次方程:(1)(2x-3)(x+1)=x+1;
(2)x2-4x+1=0.
分析 (1)先提取公因式(x+1),进而得到(2x-3-1)(x+1)=0,再解一元一次方程即可;
(2)先移项,然后进行配方,最好开方得出方程的解.
解答 解:(1)∵(2x-3)(x+1)=x+1,
∴(2x-3-1)(x+1)=0,
∴2x-4=0或x+1=0,
∴x1=2,x2=-1.
(2)∵x2-4x+1=0,
∴x2-4x=-1,
∴x2-4x+4=3,
∴(x-2)2=3,
∴x-2=$±\sqrt{3}$,
∴x1=2+$\sqrt{3}$,x2=2-$\sqrt{3}$.
点评 本题主要考查了因式分解法和配方法解一元二次方程的知识点,解答本题的关键是掌握配方法和因式分解法解一元二次方程的基本步骤,此题难度一般.

练习册系列答案
相关题目

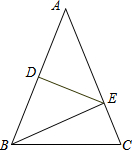 如图,己知△ABC,AB=AC,DE垂直平分AB,分别交AB、AC于D、E两点,若AB=12cm,BC=8cm,∠A=48°,求△BCE的周长和∠EBC的度数.
如图,己知△ABC,AB=AC,DE垂直平分AB,分别交AB、AC于D、E两点,若AB=12cm,BC=8cm,∠A=48°,求△BCE的周长和∠EBC的度数. 如图,你能否判断∠1+∠2与∠B+∠C的大小关系?并说明理由.
如图,你能否判断∠1+∠2与∠B+∠C的大小关系?并说明理由.