题目内容

12．（1-$\frac{1}{{2}^{2}}$）（1-$\frac{1}{{3}^{2}}$）（1-$\frac{1}{{4}^{2}}$）…（1-$\frac{1}{100{4}^{2}}$）

分析 原式利用平方差公式化简，结合后相乘即可得到结果．

解答 解：原式=（1+$\frac{1}{2}$）（1+$\frac{1}{3}$）…（1+$\frac{1}{1004}$）（1-$\frac{1}{2}$）（1-$\frac{1}{3}$）…（1-$\frac{1}{1004}$）=$\frac{3}{2}$×$\frac{4}{3}$×$\frac{5}{4}$×…×$\frac{1005}{1004}$×$\frac{1}{2}$×$\frac{2}{3}$×$\frac{3}{4}$×…×$\frac{1003}{1004}$=$\frac{1005}{2}$×$\frac{1}{1004}$=$\frac{1005}{2008}$．

点评 此题考查了平方差公式，熟练掌握平方差公式是解本题的关键．

练习册系列答案
相关题目
2．分解因式：
（1）m4-16n4；
（2）x2（x-y）+（y-x）．
3．（1）解分式方程：$\frac{x}{x-2}$-1=$\frac{6}{x+2}$；
（2）化简求值：$\frac{a-b}{a}$÷（a-$\frac{2ab-{b}^{2}}{a}$），其中a=$\sqrt{2}$，b=$\sqrt{3}$．
20．一个多项式加上3+x-2x2，得到x2-1，则这个多项式是3x2-x-4．
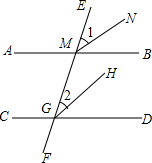7．如图，直线AB∥CD，EF分别交AB、CD于点M、G，MN平分∠EMB，GH平分∠MGD，求证：MN∥GH．
证明：∵AB∥CD已知
∴∠EMB=∠EGD两直线平行，同位角相等
∵MN平分∠EMB，GH平分∠MGD（已知）
∴∠1=$\frac{1}{2}$∠EMB，∠2=$\frac{1}{2}$∠MGD角平分线的定义
∴∠1=∠2
∴MN∥GH同位角相等，两直线平行．
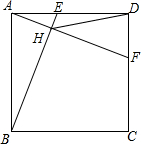17．如图，E，F是正方形ABCD边AD，CD上两个动点，且AE=DF，BE交AF于H，AB=2，连接DH．
（1）求证：AF⊥BE；
（2）求线段DH的取值范围．
4．分解因式：
（1）（2x+1）2-x2；
（2）8a-4a2-4；
（3）x4-16；                   
（4）1-a2+2ab-b2．
1．计算：
（1）-12002-$\frac{1}{7}×$[2-（-3）2]；
（2）（-2）2+（-2）÷（-$\frac{2}{3}$）+|-$\frac{1}{16}$|×（-24）；
（3）$\frac{y}{5}$-$\frac{y-1}{2}$=1-$\frac{y+2}{5}$；           
（4）6-3（x+$\frac{2}{3}$）=$\frac{2}{3}$．
2．如图，你能否判断∠1+∠2与∠B+∠C的大小关系？并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网