题目内容
20.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 10 | 5 | 2 | 1 | 2 | 5 | … |
分析 由表中对应值可得到抛物线的对称轴为直线x=2,且抛物线开口向上,由于y1<y2,则点A比点B离直线x=2要近,所以2-(m-1)>m-2,然后解不等式即可.
解答 解:∵抛物线过点(0,5)和(4,5),
∴抛物线的对称轴为直线x=2,且抛物线开口向上,
∵y1<y2,
∴点A比点B离直线x=2要近,
而m>m-1,
∴2-(m-1)>m-2,
∴m<$\frac{5}{2}$.
故答案为m<$\frac{5}{2}$.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.解题的关键是利用对应值确定对称轴,再利用二次函数的性质求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.一个圆锥的底面半径为8cm,其侧面展开图的圆心角为240°,则此圆锥的侧面积为( )
| A. | 96πcm2 | B. | 48πcm2 | C. | 36πcm2 | D. | 24πcm2 |
15.下列运算中,结果正确的是( )
| A. | a4+a4=a8 | B. | a2•a3=a5 | C. | 2x+3y=5xy | D. | (-2a2)3=-6a6 |
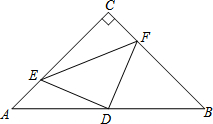 如图,在△ABC中,∠C=90°,AC=BC=2$\sqrt{2}$,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DFE是等腰直角三角形;②四边形CEDF的周长不变;③点C到线段EF的最大距离为1.其中正确的结论有①③.(填写所有正确结论的序号)
如图,在△ABC中,∠C=90°,AC=BC=2$\sqrt{2}$,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DFE是等腰直角三角形;②四边形CEDF的周长不变;③点C到线段EF的最大距离为1.其中正确的结论有①③.(填写所有正确结论的序号)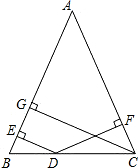 如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.DE,DF,CG的长之间存在着怎样的等量关系?并加以证明.
如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.DE,DF,CG的长之间存在着怎样的等量关系?并加以证明.