题目内容
8.(1)计算:(1-$\sqrt{2}$)0-tan60°+($\frac{1}{2}$)-1(2)解方程组:$\left\{\begin{array}{l}{x+y=4}\\{2x-y=5}\end{array}\right.$.
分析 (1)原式第一项利用零指数幂法则计算,第二项利用特殊角的三角函数值计算,第三项利用负指数幂法则计算即可得到结果;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)原式1-$\sqrt{3}$+2=3-$\sqrt{3}$;
(2)$\left\{\begin{array}{l}{x+y=4①}\\{2x-y=5②}\end{array}\right.$,
①+②得:3x=9,即x=3,
把x=3代入①得:y=1,
则不等式组的解集为$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
3. 如图所示的平面图形能折叠成的长方体是( )
如图所示的平面图形能折叠成的长方体是( )
 如图所示的平面图形能折叠成的长方体是( )
如图所示的平面图形能折叠成的长方体是( )| A. |  | B. |  | C. |  | D. |  |
20.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:
若A(m,y),B(m-1,y2)两点都在该函数的图象上,当m满足范围m<$\frac{5}{2}$时,y1<y2.
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 10 | 5 | 2 | 1 | 2 | 5 | … |
17.-6的倒数是( )
| A. | 6 | B. | $\frac{1}{6}$ | C. | -$\frac{1}{6}$ | D. | -6 |
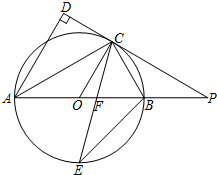 如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB点F,连接BE.
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB点F,连接BE. 如图,一堤坝的坡角∠ABC=60°,坡面长度AB=24米(图为横截面).为了使堤坝更加牢固,需要改变堤坝的坡面,为使得坡面的坡角∠ADB=50°,则应将堤坝底端向外拓宽(BD)多少米?(结果精确到0.1米)
如图,一堤坝的坡角∠ABC=60°,坡面长度AB=24米(图为横截面).为了使堤坝更加牢固,需要改变堤坝的坡面,为使得坡面的坡角∠ADB=50°,则应将堤坝底端向外拓宽(BD)多少米?(结果精确到0.1米) 如图,在?ABEF中,AB=2,AF<AB.现将线段EF在直线EF上移动,在移动过程中,设线段EF的对应线段为CD,连接AD、BC.
如图,在?ABEF中,AB=2,AF<AB.现将线段EF在直线EF上移动,在移动过程中,设线段EF的对应线段为CD,连接AD、BC.