题目内容
13．
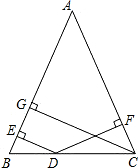如图，在△ABC中，AB=AC，D是BC上任意一点，过D分别向AB，AC引垂线，垂足分别为E，F，CG是AB边上的高．DE，DF，CG的长之间存在着怎样的等量关系？并加以证明．
分析 连接AD，然后根据S△ABC=S△ABD+S△ACD列方程整理即可得解．
解答 
解：CG=DE+DF．
理由如下：如图，连接AD，
∵S△ABC=S△ABD+S△ACD，
∴$\frac{1}{2}$AB•CG=$\frac{1}{2}$AC•DE+$\frac{1}{2}$AB•DF，
∴AB=AC，
∴CG=DE+DF．
点评 本题考查了等腰三角形的性质，作辅助线，把△ABC分成两个三角形，然后利用三角形的面积列出方程是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
20．已知二次函数y=ax2+bx+c中，函数y与自变量x的部分对应值如下表：
若A（m，y），B（m-1，y2）两点都在该函数的图象上，当m满足范围m＜$\frac{5}{2}$时，y1＜y2．
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 10 | 5 | 2 | 1 | 2 | 5 | … |
如图，在?ABEF中，AB=2，AF＜AB．现将线段EF在直线EF上移动，在移动过程中，设线段EF的对应线段为CD，连接AD、BC．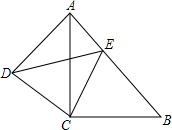
如图，在四边形ABCD中，连接AC，AC=BC，E是AB上一点，且有CE=CD，AD=BE．
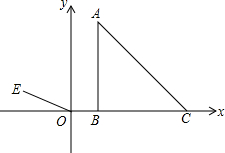如图，在平面直角坐标系中，已知点E（-2，1），连结OE，△ABC的三个顶点坐标分别为A（1，4），B（1，0），C（5，0）．