题目内容
17. 如图,某居民小区有一栋居民楼,在该楼的前面32米处要再盖一栋30米的新楼,现需了解新楼对采光的影响,当冬季正午的阳光与水平线的夹角为37°时,求新楼的影子在居民楼上有多高?
如图,某居民小区有一栋居民楼,在该楼的前面32米处要再盖一栋30米的新楼,现需了解新楼对采光的影响,当冬季正午的阳光与水平线的夹角为37°时,求新楼的影子在居民楼上有多高?(参考数值:sin37°≈$\frac{3}{5}$,cos37°≈$\frac{4}{5}$,tan37°≈$\frac{3}{4}$)
分析 光线交CD于点E,过点E作EF⊥AB,可得矩形BDEF,设DE=x米,则AF=(30-x)米,在RT△AFE中根据tan37°=$\frac{AF}{EF}$列出关于x的方程,解方程可得答案.
解答 解:如图,光线交CD于点E,过点E作EF⊥AB,交AB于点F,
由题意知,AB⊥BD,CD⊥BD,
∴∠ABD=∠CDB=∠EFB=∠AFE=90°,
∴四边形BDEF是矩形,
∴BD=EF=32米,FB=DE,
设DE=x米,则AF=(30-x)米,
在RT△AFE中,∵∠AEF=37°,
∴tan37°=$\frac{AF}{EF}$,
即:$\frac{3}{4}$=$\frac{30-x}{32}$,
解得:x=6,
答:新楼的影子在居民楼上的高为6米.
点评 本题考查的是解直角三角形的应用,掌握锐角三角函数的概念、正确作出辅助线构造直角三角形是解题的关键.

练习册系列答案
相关题目
5.下列图形中,是中心对称图形,但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
12.下列二次根式中,属于最简二次根式的是( )
| A. | $\sqrt{48}$ | B. | $\sqrt{\frac{a}{b}}$ | C. | $\sqrt{4a+4}$ | D. | $\sqrt{14}$ |
9.济南市名校德润中学九年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了$\frac{1}{3}$小时后,其余学生乘汽车出发,结果他们同时达到,已知乘汽车学生的速度是骑车学生速度的2倍,求骑车学生的速度.设骑车学生的速度为每小时x千米,则所列方程正确的是( )
| A. | $\frac{10}{x}=\frac{10}{2x}+\frac{1}{3}$ | B. | $\frac{10}{2x}=\frac{10}{x}+\frac{1}{3}$ | C. | $\frac{10}{x}=\frac{1}{3}-\frac{10}{2x}$ | D. | $\frac{10}{2x}-\frac{1}{3}=\frac{10}{x}$ |
 如图,DE∥BC,BE平分∠ABC,若∠ADE=60°,则∠1=30°.
如图,DE∥BC,BE平分∠ABC,若∠ADE=60°,则∠1=30°. 在平面直角坐标系中,顺次连结点A(-2,0)、B(0,-2)、C(2,0)、D(0,2)所得的四边形ABCD是怎样的四边形?并说明理由.
在平面直角坐标系中,顺次连结点A(-2,0)、B(0,-2)、C(2,0)、D(0,2)所得的四边形ABCD是怎样的四边形?并说明理由.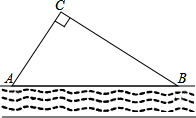 某校生物兴趣小组把一块沿河的三角形废地(如图)开辟为生物园(设AB段河岸为直线),已知∠ACB=90°,∠CAB=55°,BC=80米,学校决定在点C处建一个蓄水池,利用管道从河中取水,已知每铺设1米管道费用为50元,求铺设管道的最低费用(精确到1元).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
某校生物兴趣小组把一块沿河的三角形废地(如图)开辟为生物园(设AB段河岸为直线),已知∠ACB=90°,∠CAB=55°,BC=80米,学校决定在点C处建一个蓄水池,利用管道从河中取水,已知每铺设1米管道费用为50元,求铺设管道的最低费用(精确到1元).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43) 如图,由五个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体的主视图和左视图的面积之和是7.
如图,由五个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体的主视图和左视图的面积之和是7.