题目内容
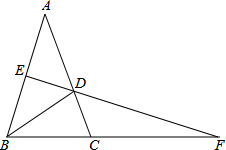 如图,在△ABC中,AB=AC,∠A=36°,BD是∠B的平分线,交AC于点D,E是AB中点,ED交BC的延长线于点F.求证:AB=CF.
如图,在△ABC中,AB=AC,∠A=36°,BD是∠B的平分线,交AC于点D,E是AB中点,ED交BC的延长线于点F.求证:AB=CF.考点:等腰三角形的判定与性质,线段垂直平分线的性质
专题:证明题
分析:根据等腰三角形的性质,可得∠ABC=∠ACB=72°,根据角平分线的性质,可得∠1=∠2=36°,可得DA与DB的关系,根据线段垂直平分线的判定与性质,可得FA与FB的关系,可得∠FAB与∠ABC的关系,根据三角形外角的关系,可得∠AFC=∠ACB-∠3=36°,根据等腰三角形的判定,可得AC与CF的关系,根据等量代换,可得答案.
解答:证明:如图:
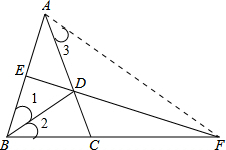 ,
,
连接AF,
∵AB=AC,∠BAC=36°,
∴∠ABC=∠ACB=72°.
∵BD平分∠ABC,
∴∠1=∠2=36°,
∴∠1=∠BAD=36°,
∴DA=DB.
∵AE=BE,
∴FE⊥AB,即FE是AB的垂直平分线,
∴FA=FB,
∴∠FAB=∠ABC=72°,
∴∠3=∠FAB-∠BAC=36°,
∵∠ACB=∠3+∠AFC,
∴∠AFC=∠ACB-∠3=36°,
∴∠3=∠AFC,
∴AC=CF,
∴AB=CF.
 ,
,连接AF,
∵AB=AC,∠BAC=36°,
∴∠ABC=∠ACB=72°.
∵BD平分∠ABC,
∴∠1=∠2=36°,
∴∠1=∠BAD=36°,
∴DA=DB.
∵AE=BE,
∴FE⊥AB,即FE是AB的垂直平分线,
∴FA=FB,
∴∠FAB=∠ABC=72°,
∴∠3=∠FAB-∠BAC=36°,
∵∠ACB=∠3+∠AFC,
∴∠AFC=∠ACB-∠3=36°,
∴∠3=∠AFC,
∴AC=CF,
∴AB=CF.
点评:本题考查了等腰三角形的判定与性质,利用了等腰三角形的判定与性质,线段垂直平分线的判定与性质,三角形外角的性质.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 如图,在等腰梯形ABCD中,AB∥CD,AD=BC,∠ACB=90°,∠B=60°,DC=2cm,求AB的长.
如图,在等腰梯形ABCD中,AB∥CD,AD=BC,∠ACB=90°,∠B=60°,DC=2cm,求AB的长.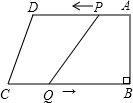 如图,已知梯形ABCD中,AD∥BC,∠B=90°,AD=21cm,BC=24cm,动点P从点A出发,以1cm/s的速度沿边AD向D运动,另一动点Q同时从C出发,以2cm/s的速度沿边CB向点B运动,其中一动点达到端点时,另一动点随之停止运动.设点P的运动时间为t秒.问:
如图,已知梯形ABCD中,AD∥BC,∠B=90°,AD=21cm,BC=24cm,动点P从点A出发,以1cm/s的速度沿边AD向D运动,另一动点Q同时从C出发,以2cm/s的速度沿边CB向点B运动,其中一动点达到端点时,另一动点随之停止运动.设点P的运动时间为t秒.问: 如图,△ABC中,BE平分∠ABC,DE∥BC交AB于D,AC=12,AB=9,AE=4,求DE的值.
如图,△ABC中,BE平分∠ABC,DE∥BC交AB于D,AC=12,AB=9,AE=4,求DE的值.
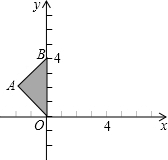 在平面直角坐标系中,等腰Rt△OAB斜边OB在y轴上,且OB=4.
在平面直角坐标系中,等腰Rt△OAB斜边OB在y轴上,且OB=4.