题目内容
已知∠ABC,∠ACB的平分线交于I.
(1)根据下列条件分别求出∠BIC的度数:
①∠ABC=70°,∠ACB=50°;②∠ACB+∠ABC=120°;③∠A=90°;④∠A=n°.
(2)你能发现∠BIC与∠A的关系吗?
(1)根据下列条件分别求出∠BIC的度数:
①∠ABC=70°,∠ACB=50°;②∠ACB+∠ABC=120°;③∠A=90°;④∠A=n°.
(2)你能发现∠BIC与∠A的关系吗?
考点:三角形内角和定理
专题:
分析:(1)①已知∠ABC,∠ACB,由内角和定理求∠BAC,再根据角平分线性质求∠IBC+∠ICB,在△IBC中,由内角和定理求∠BIC的度数;
②已知∠ABC+∠ACB,由内角和定理求∠BAC,再根据角平分线性质求∠IBC+∠ICB,在△IBC中,由内角和定理求∠BIC的度数;
③已知∠A,由内角和定理求∠ABC+∠ACB,再根据角平分线性质求∠IBC+∠ICB,在△IBC中,由内角和定理求∠BIC的度数;
④已知∠A,由内角和定理求∠ABC+∠ACB,再根据角平分线性质求∠IBC+∠ICB,在△IBC中,由内角和定理求∠BIC的度数;
(2)∠BIC的大小不发生变化.可由角平分线的性质及三角形内角和定理求出∠BIC=90°+
∠A.
②已知∠ABC+∠ACB,由内角和定理求∠BAC,再根据角平分线性质求∠IBC+∠ICB,在△IBC中,由内角和定理求∠BIC的度数;
③已知∠A,由内角和定理求∠ABC+∠ACB,再根据角平分线性质求∠IBC+∠ICB,在△IBC中,由内角和定理求∠BIC的度数;
④已知∠A,由内角和定理求∠ABC+∠ACB,再根据角平分线性质求∠IBC+∠ICB,在△IBC中,由内角和定理求∠BIC的度数;
(2)∠BIC的大小不发生变化.可由角平分线的性质及三角形内角和定理求出∠BIC=90°+
| 1 |
| 2 |
解答:解:(1)①∵在△ABC中,∠ABC=70°,∠ACB=50°,
∴∠BAC=180°-∠ABC-∠ACB=60°,
∵BD、CE分别是∠ABC、∠ACB的平分线,
∴∠IBC=
∠ABC=35°,∠ICB=
∠ACB=25°,
∴∠BIC=180°-∠IBC-∠ICB=120°;
②∵在△ABC中,∠ABC+∠ACB=120°,
∴∠BAC=180°-∠ABC-∠ACB=60°,
∵BD、CE分别是∠ABC、∠ACB的平分线,
∴∠IBC=
∠ABC,∠ICB=
∠ACB,
∴∠BIC=180°-∠IBC-∠ICB=120°;
③∵∠A=90°,
∴∠ABC+∠ACB=90°,
∵BD、CE分别是∠ABC、∠ACB的平分线,
∴∠IBC=
∠ABC,∠ICB=
∠ACB,
∴∠BIC=180°-∠IBC-∠ICB=135°;
④∵∠A=n°,
∴∠ABC+∠ACB=180°-n°,
∵BD、CE分别是∠ABC、∠ACB的平分线,
∴∠IBC=
∠ABC,∠ICB=
∠ACB,
∴∠BIC=180°-∠IBC-∠ICB=90°+
n°;
(2)∠BIC的大小不发生变化.
∵BD、CE分别是∠ABC、∠ACB的平分线,
∴∠IBC=
∠ABC,∠ICB=
∠ACB,
∴∠BIC=180°-∠IBC-∠ICB,
=180°-
(∠ABC+∠ACB),
=180°-
(180°-∠A),
=90°+
∠A,
∴∠BAC=180°-∠ABC-∠ACB=60°,
∵BD、CE分别是∠ABC、∠ACB的平分线,
∴∠IBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BIC=180°-∠IBC-∠ICB=120°;
②∵在△ABC中,∠ABC+∠ACB=120°,
∴∠BAC=180°-∠ABC-∠ACB=60°,
∵BD、CE分别是∠ABC、∠ACB的平分线,
∴∠IBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BIC=180°-∠IBC-∠ICB=120°;
③∵∠A=90°,
∴∠ABC+∠ACB=90°,
∵BD、CE分别是∠ABC、∠ACB的平分线,
∴∠IBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BIC=180°-∠IBC-∠ICB=135°;
④∵∠A=n°,
∴∠ABC+∠ACB=180°-n°,
∵BD、CE分别是∠ABC、∠ACB的平分线,
∴∠IBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BIC=180°-∠IBC-∠ICB=90°+
| 1 |
| 2 |
(2)∠BIC的大小不发生变化.
∵BD、CE分别是∠ABC、∠ACB的平分线,
∴∠IBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BIC=180°-∠IBC-∠ICB,
=180°-
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
点评:本题考查了三角形的内角和定理,解题的关键是利用三角形内角和定理和已知条件列方程组求解计算.

练习册系列答案
相关题目
已知点M(-2,3)在双曲线y=
上,则下列各点一定在该双曲线上的是( )
| k |
| x |
| A、(3,-2) |
| B、(-2,-3) |
| C、(2,3) |
| D、(3,2) |
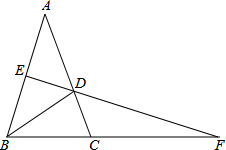 如图,在△ABC中,AB=AC,∠A=36°,BD是∠B的平分线,交AC于点D,E是AB中点,ED交BC的延长线于点F.求证:AB=CF.
如图,在△ABC中,AB=AC,∠A=36°,BD是∠B的平分线,交AC于点D,E是AB中点,ED交BC的延长线于点F.求证:AB=CF. 如图,某人在D处测得山顶C的仰角为30°,向前走200米来到山脚A处,测得山坡AC的坡度为i=
如图,某人在D处测得山顶C的仰角为30°,向前走200米来到山脚A处,测得山坡AC的坡度为i=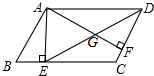 如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥DC于F,∠BAE=30°,BE=2,CF=1.
如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥DC于F,∠BAE=30°,BE=2,CF=1.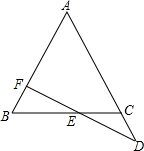 如图,在△ABC中,AB=AC,直线FD交AB于点F,交BC于点E,交AC的延长线于点D,且CD=BF,求证:FE=ED.
如图,在△ABC中,AB=AC,直线FD交AB于点F,交BC于点E,交AC的延长线于点D,且CD=BF,求证:FE=ED.