题目内容
3.在△ABC中,∠CAB=120°,AB=AC=10$\sqrt{3}$cm,动点P从点C出发,沿CB以每秒2cm的速度向B移动,当PA和△ABC的腰垂直时,点P移动的时间至少是5秒.分析 在△ABC中,∠BAC=120°,AB=AC,可得∠B=∠C=30°,过点A作AD⊥BC于D,即可得出BC的长,本题主要分两种情况,
①当PA⊥AC,即有PC=2AP,利用勾股定理即可得出PC的长,即可得出BP;
②当PA垂直AB时,解答同①.
解答  解:过点A作AD⊥BC于点D,根据题意,可得BD=15,即BC=30;
解:过点A作AD⊥BC于点D,根据题意,可得BD=15,即BC=30;
①当PA⊥AC,即PC=2AP,
在Rt△PAC中,可得PC=20,BP=10,即此时点P经过5秒.
②当PA⊥AB时,即PB=2AP,在Rt△PAB中,可得PB=20,即点P已经经过10秒.
∴点P移动的时间至少是5秒,
故答案为:5.
点评 本题主要考查是解含有30°角的直角三角形,要求学生能够熟练应用.

练习册系列答案
相关题目
2.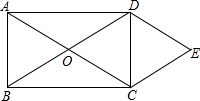 如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
(1)若AB=6,BC=8,求四边形OCED的面积.
(2)若∠ACB=30°,菱形OCED的面积为18$\sqrt{3}$,求AC的长.
 如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.(1)若AB=6,BC=8,求四边形OCED的面积.
(2)若∠ACB=30°,菱形OCED的面积为18$\sqrt{3}$,求AC的长.
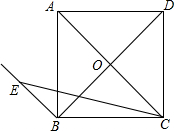 如图,四边形ABCD为正方形,EB∥AC,EC=AC,E在FB上,求∠ECB的度数.
如图,四边形ABCD为正方形,EB∥AC,EC=AC,E在FB上,求∠ECB的度数.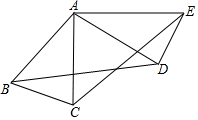 如图,△ABC中,AB=AC,∠ABC=70°.△ABC绕点A按逆时针方向旋转一定角度后,得到△ADE.问:
如图,△ABC中,AB=AC,∠ABC=70°.△ABC绕点A按逆时针方向旋转一定角度后,得到△ADE.问: 如图,有一条小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,AE∥CF,则这条小路AECF的面积是多少?
如图,有一条小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,AE∥CF,则这条小路AECF的面积是多少?