��Ŀ����
18����֪��ͼ��ֱ��y=kx+b��x�ᡢy��ֱ��ڵ�A��B����ֱ��y=3x���ڵ�C����|OA-6|+$\sqrt{OB-\frac{9}{2}}$=0����ֱ��y=kx+b��ֱ��y=3x�۵�����x�ύ�ڵ�D����y�ύ�ڵ�E����1����ֱ��y=kx+b�Ľ���ʽ����C�����ꣻ
��2�����BCE�������
��3������P��ֱ��y=3x�ϵ�һ�����㣬��ƽ�����Ƿ����һ��Q��ʹ�Ե�A��C��P��QΪ������ı����Ǿ��Σ������ڣ���ֱ��д����P����Q�����ꣻ�������ڣ���˵�����ɣ�
���� ��1�����÷Ǹ������OA��OB�������ó���A��B���꣬�ô���ϵ�������ֱ��AB����ʽ��������ֱ��OC�Ľ���ʽ���������C�����ꣻ
��2������ֱ��MN��ֱ��AB�Ľ���ʽ�����M�����꣬���öԳ������N�����꣬�������ֱ��CE�Ľ���ʽ���ɣ�
��3����ACΪ���εıߺͶԽ��ߣ����þ��εĶԽ�����ƽ������ȣ������е����깫ʽ���ɽ����
��� �⣺��1����|OA-6|+$\sqrt{OB-\frac{9}{2}}$=0��
��OA=6��OB=$\frac{9}{2}$��
��A��-6��0����B��0��$\frac{9}{2}$����
��$\left\{\begin{array}{l}{-6k+b=0}\\{b=\frac{9}{2}}\end{array}\right.$��
��$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=\frac{9}{2}}\end{array}\right.$��
��ֱ��AB�Ľ���ʽΪy=$\frac{3}{4}$x+$\frac{9}{2}$�٣�
�ߵ�C��ֱ��AB��OC��y=3x�ڵĽ��㣬
�����٢ڽ�ã�$\left\{\begin{array}{l}{x=2}\\{y=6}\end{array}\right.$��
��C��2��6����
��2����ͼ1��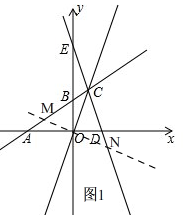
����O��ֱ��MN��OC��ֱ��AB��M��ֱ��CE��N��
��ֱ��OC�Ľ���ʽΪy=3x��
��ֱ��MN�Ľ���ʽΪy=-$\frac{1}{3}$x�٣�
��ֱ��AB�Ľ���ʽΪy=$\frac{3}{4}$x+$\frac{9}{2}$�ڣ�
�����٢ڽ�ã�x=-$\frac{54}{13}$��y=$\frac{18}{13}$��
��M��-$\frac{54}{13}$��$\frac{18}{13}$����
���۵�֪��M��N����ԭ��Գƣ�
��N��$\frac{54}{13}$��-$\frac{18}{13}$����
��C��2��6����
��ֱ��CE�Ľ���ʽΪy=-$\frac{24}{7}$x+$\frac{90}{7}$��
��E��0��$\frac{90}{7}$����
��BE=$\frac{90}{7}$-$\frac{9}{2}$=$\frac{117}{14}$��
��S��BCE=$\frac{1}{2}$BE��|xC|=$\frac{1}{2}��\frac{117}{14}$��2=$\frac{117}{14}$��
��3����ͼ2��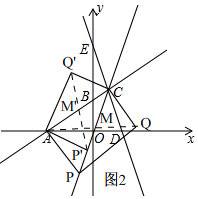
��ACΪ���εı�ʱ��AP��AC��
��ֱ��AC�Ľ���ʽΪy=$\frac{3}{4}$x+$\frac{9}{2}$��
��ֱ��AP�Ľ���ʽΪy=-$\frac{4}{3}$x-8��
�ߵ�P��ֱ��y=3x���ϣ�
�����٢ڽ�ã�P��-$\frac{24}{13}$��-$\frac{72}{13}$����
��C��2��6��
��PC���е�M��$\frac{1}{13}$��$\frac{3}{13}$����
���ı���APQC�Ǿ��Σ�
��M��AQ���е㣬
��Q��$\frac{80}{13}$��$\frac{6}{13}$����
��ACΪ���εĶԽ���ʱ��AP'��OC��
��ֱ��OC�Ľ���ʽΪy=3x��
��ֱ��AP'�Ľ���ʽΪy=-$\frac{1}{3}$x-2�ۣ�
�ߵ�P'��ֱ��OC�ϣ�
���P'����������y=3x�ܣ������ۢܽ�ã�P'��-$\frac{3}{5}$��-$\frac{9}{5}$����
��A��-6��0����C��2��6����
��AC�������M'��-2��3����
���ı���AP'CQ'�Ǿ��Σ�
��M'��P'Q'���е㣬
��Q'��-$\frac{17}{5}$��$\frac{39}{5}$����
�������������ĵ�P��-$\frac{24}{13}$��-$\frac{72}{13}$����Q��$\frac{80}{13}$��$\frac{6}{13}$����P��-$\frac{3}{5}$��-$\frac{9}{5}$����Q��-$\frac{17}{5}$��$\frac{39}{5}$����
���� ������һ�κ����ۺ��⣬��Ҫ�����˷Ǹ��ԣ�����ϵ�����������ε������ʽ�����ε����ʣ��۵������ʣ��Ȿ��Ĺؼ������ô���ϵ������ֱ�߽���ʽ���⣨3���Ĺؼ��Ƿ������۵�˼��˼�����⣮

 ��ͼ����?ABCD�У�BC=20$\sqrt{2}$cm��CD=20cm����A=45�㣬����P�ӵ�B��������BC���C�˶�������Q�ӵ�D��������DB���B�˶�����P�͵�Q���˶��ٶȷֱ�Ϊ3$\sqrt{2}$cm/s��2cm/s��һ��ֹͣ�˶�������һ��Ҳ��ֹ֮ͣ������BPQ��ֱ��������ʱ����Ҫ������������
��ͼ����?ABCD�У�BC=20$\sqrt{2}$cm��CD=20cm����A=45�㣬����P�ӵ�B��������BC���C�˶�������Q�ӵ�D��������DB���B�˶�����P�͵�Q���˶��ٶȷֱ�Ϊ3$\sqrt{2}$cm/s��2cm/s��һ��ֹͣ�˶�������һ��Ҳ��ֹ֮ͣ������BPQ��ֱ��������ʱ����Ҫ������������| A�� | 4s | B�� | $\frac{5}{2}$s | C�� | $\frac{5}{2}$s��4s | D�� | 6s |
| A�� | k��2��m��0 | B�� | k��2��m��0 | C�� | k��2��m��0 | D�� | k��2��m��0 |
| A�� | 1��1��$\sqrt{2}$ | B�� | 2��3��4 | C�� | 4��5��6 | D�� | 6��8��11 |
 ��֪�ھ���ABCD�У�AB=9��AD=6����E�ڱ�CD���ƶ�����AE���۾��Σ�ʹ�õ�D���ڵ�F������ôCF����Сֵ��3$\sqrt{13}$-6��
��֪�ھ���ABCD�У�AB=9��AD=6����E�ڱ�CD���ƶ�����AE���۾��Σ�ʹ�õ�D���ڵ�F������ôCF����Сֵ��3$\sqrt{13}$-6�� ��ͼ��ʾ��ֱ��AB��CD�ཻ�ڵ�O������AOD���BOC�ĺ�Ϊ236�㣬���AOC�Ķ���Ϊ62�㣮
��ͼ��ʾ��ֱ��AB��CD�ཻ�ڵ�O������AOD���BOC�ĺ�Ϊ236�㣬���AOC�Ķ���Ϊ62�㣮