题目内容
8.以下列各组数为边长能构成直角三角形的是( )| A. | 1,1,$\sqrt{2}$ | B. | 2,3,4 | C. | 4,5,6 | D. | 6,8,11 |
分析 根据勾股定理的逆定理对各选项进行逐一判断即可.
解答 解:A、∵12+12=2=($\sqrt{2}$)2,∴能构成直角三角形,故本选项正确;
B、∵22+32=25≠42,∴不能构成直角三角形,故本选项错误;
C、∵42+52=41≠62,∴不能构成直角三角形,故本选项错误;
D、∵62+82=100≠112,∴不能构成直角三角形,故本选项错误.
故选A.
点评 本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.

练习册系列答案
相关题目
3.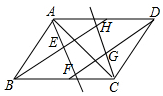 如图,已知?ABCD的四个内角的平分线分别相交于点E、F、G、H,连接AC.若EF=2,FG=GC=5,则AC的长是( )
如图,已知?ABCD的四个内角的平分线分别相交于点E、F、G、H,连接AC.若EF=2,FG=GC=5,则AC的长是( )
 如图,已知?ABCD的四个内角的平分线分别相交于点E、F、G、H,连接AC.若EF=2,FG=GC=5,则AC的长是( )
如图,已知?ABCD的四个内角的平分线分别相交于点E、F、G、H,连接AC.若EF=2,FG=GC=5,则AC的长是( )| A. | 12 | B. | 13 | C. | $6\sqrt{5}$ | D. | $8\sqrt{3}$ |
17.下列四个命题是真命题的是( )
| A. | 内错角相等 | |
| B. | 如果两个角的和是180°,那么这两个角是邻补角 | |
| C. | 在同一平面内,平行于同一条直线的两条直线互相平行 | |
| D. | 在同一平面内,垂直于同一条直线的两条直线互相垂直 |
18.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{\frac{1}{9}}$ | C. | $\sqrt{{a}^{2}}$ | D. | $\sqrt{{a}^{2}+1}$ |
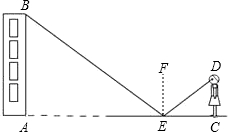 小玲用下面的方法来测量学校教学大楼AB的高度:如图,在水平面上放一面平面镜,镜子与教学楼的距离EA=12米,当她与镜子的距离CE=2米时,她刚好能从镜子中看到教学楼的顶端B.已知她的眼睛距地面的高度DC=1.5米.请你帮助小玲计算出教学楼的高度AB是多少米(根据光的反射定律:反射角等于入射角.)
小玲用下面的方法来测量学校教学大楼AB的高度:如图,在水平面上放一面平面镜,镜子与教学楼的距离EA=12米,当她与镜子的距离CE=2米时,她刚好能从镜子中看到教学楼的顶端B.已知她的眼睛距地面的高度DC=1.5米.请你帮助小玲计算出教学楼的高度AB是多少米(根据光的反射定律:反射角等于入射角.)