题目内容
8. 已知在矩形ABCD中,AB=9,AD=6,点E在边CD上移动,沿AE翻折矩形,使得点D落在点F处,那么CF的最小值是3$\sqrt{13}$-6.
已知在矩形ABCD中,AB=9,AD=6,点E在边CD上移动,沿AE翻折矩形,使得点D落在点F处,那么CF的最小值是3$\sqrt{13}$-6.
分析 当△ADE沿AE翻折时,点D落在AC上时,有CF最小,根据勾股定理先求AC的长,相减可得FC的最小值.
解答  解:当点F落在对角线AC上,即A,F,C三点共线时,CF的值最小,
解:当点F落在对角线AC上,即A,F,C三点共线时,CF的值最小,
∵在矩形ABCD中,AB=9,AD=6,
∴BC=AD=6,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=3$\sqrt{13}$,
由折叠的性质得,AF=AD=6,
∴CF=AC-AF=3$\sqrt{13}$-6,
故答案为:3$\sqrt{13}$-6.
点评 本题考查的是翻折变换的性质,翻折变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等,解题的关键是确定其最小值的位置,再利用勾股定理的折叠性质进行计算.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
20.下列各对x,y的值中,不是方程3x+4y=5的解的是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=\frac{1}{2}}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=0}\\{y=\frac{5}{4}}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=\frac{2}{5}}\\{y=0}\end{array}\right.$ |
18.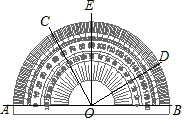 如图所示,用量角器度量几个角的度数.下列结论中正确的是( )
如图所示,用量角器度量几个角的度数.下列结论中正确的是( )
 如图所示,用量角器度量几个角的度数.下列结论中正确的是( )
如图所示,用量角器度量几个角的度数.下列结论中正确的是( )| A. | ∠BOC=60° | B. | ∠COA是∠EOD的余角 | ||
| C. | ∠AOC=∠BOD | D. | ∠AOD与∠COE互补 |
13.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
17.下列方程组中,是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{x+y=5}\\{z+x=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+\frac{1}{y}=1}\\{\frac{1}{x}-y=3}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x-y+xy=4}\\{3x-y=4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{1}{2}x-2y=15}\\{\frac{1}{3}x+\frac{1}{2}y=4}\end{array}\right.$ |
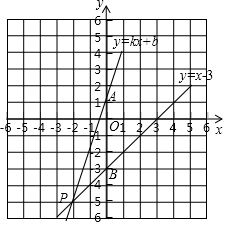 如图,已知一次函数y=kx+b经过点A(0,1)且和直线y=x-3交于点P(a,-5).
如图,已知一次函数y=kx+b经过点A(0,1)且和直线y=x-3交于点P(a,-5).