题目内容
20.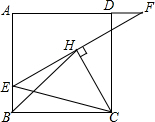 如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且BE=DF,连接EF;作CH⊥EF,连接CE、BH,若BH=8,EF=4$\sqrt{10}$,则正方形ABCD的边长是( )
如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且BE=DF,连接EF;作CH⊥EF,连接CE、BH,若BH=8,EF=4$\sqrt{10}$,则正方形ABCD的边长是( )| A. | 5$\sqrt{2}$ | B. | 6$\sqrt{2}$ | C. | 5$\sqrt{5}$ | D. | 6$\sqrt{5}$ |
分析 连接AH,AC,CF,BH与AC交于M,推出△BCE≌△CDF,由全等三角形的性质得到CE=CF,∠BCE=∠DCF,求得∠ECF=90°,根据直角三角形的性质得到CH=EH=HF=$\frac{1}{2}$EF=2$\sqrt{10}$,证得BH垂直平分AC,得到AM=BM=CM=$\frac{1}{2}$AC=$\frac{\sqrt{2}}{2}$x,设BC=x,根据勾股定理得到HM=$\sqrt{C{H}^{2}-C{M}^{2}}$=$\sqrt{40-\frac{1}{2}{x}^{2}}$,列方程即可得到结论.
解答 解:连接AH,AC,CF,BH与AC交于M,
∵在正方形ABCD中,BC=CD,∠ABC=∠ADC=90°∴∠CDF=90°,
在△BCE与△CDF中,$\left\{\begin{array}{l}{BE=CF}\\{∠ABBC=∠CDF=90°}\\{BC=CD}\end{array}\right.$,
∴△BCE≌△CDF,
∴CE=CF,∠BCE=∠DCF,
∵∠BCE+∠ECD=∠ECD+∠DCF=90°,
∴∠BCE=∠DCF,
∴∠ECF=90°,
∴CH=EH=HF=$\frac{1}{2}$EF=2$\sqrt{10}$,
∴AH=$\frac{1}{2}$EF,
∴AH=CH,
∵AB=BC,
∴BH垂直平分AC,
∴AM=BM=CM=$\frac{1}{2}$AC=$\frac{\sqrt{2}}{2}$x,
设BC=x,
∴BM=CM=$\frac{\sqrt{2}}{2}$x,
HM=$\sqrt{C{H}^{2}-C{M}^{2}}$=$\sqrt{40-\frac{1}{2}{x}^{2}}$,
∵BH=8,
∴$\frac{\sqrt{2}}{2}$x+$\sqrt{40-\frac{1}{2}{x}^{2}}$=8,
∴x=6$\sqrt{2}$或x=2$\sqrt{2}$(不合题意舍去),
∴BC=6$\sqrt{2}$,
∴正方形ABCD的边长是6$\sqrt{2}$.
故选B.
点评 本题考查了全等三角形的判定和性质,勾股定理,正方形的性质,正确的作出辅助线是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,点O在直线AB上,CO⊥DO,垂足为O,则∠1与∠2的度数和为( )
如图,点O在直线AB上,CO⊥DO,垂足为O,则∠1与∠2的度数和为( )| A. | 45° | B. | 60° | C. | 90° | D. | 无法确定 |
 如图,⊙O中,AB,AC是弦,点M是$\widehat{CAB}$的中点,MP⊥AB,垂足为P,若AC=1,AP=2,则PB的长为4.
如图,⊙O中,AB,AC是弦,点M是$\widehat{CAB}$的中点,MP⊥AB,垂足为P,若AC=1,AP=2,则PB的长为4.