题目内容
12.运用完全平方公式计算:(1)(3a+b)2
(2)($\frac{1}{2}$x-2y)2
(3)(-x-y)2
(4)1992.
分析 (1)直接利用完全平方公式计算得出答案;
(2)直接利用完全平方公式计算得出答案;
(3)直接利用完全平方公式计算得出答案;
(4)直接将原式变形,再利用完全平方公式计算得出答案.
解答 解:(1)(3a+b)2=9a2+6ab+b2;
(2)($\frac{1}{2}$x-2y)2=$\frac{1}{4}$x2-2xy+4y2;
(3)(-x-y)2=x2+2xy+y2;
(4)1992=(200-1)2=40000-400+1=399601.
点评 此题主要考查了完全平方公式的应用,熟练应用完全平方公式是解题关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
2.已知二次函数y=a(x-1)2+b(a≠0)有最大值2,则a、b的大小比较为( )
| A. | a>b | B. | a<b | C. | a=b | D. | 不能确定 |
3.在平面直角坐标系xOy中,经过点(sin45°,cos30°)的直线,与以原点为圆心,2为半径的圆的位置关系是( )
| A. | 相交 | B. | 相切 | ||
| C. | 相离 | D. | 以上三者都有可能 |
17.抛物线y=2x2+4x+1与x轴( )
| A. | 无交点 | B. | 只有一个交点 | ||
| C. | 有两个不同的交点 | D. | 有三个不同的交点 |
20.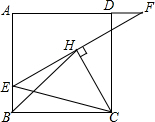 如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且BE=DF,连接EF;作CH⊥EF,连接CE、BH,若BH=8,EF=4$\sqrt{10}$,则正方形ABCD的边长是( )
如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且BE=DF,连接EF;作CH⊥EF,连接CE、BH,若BH=8,EF=4$\sqrt{10}$,则正方形ABCD的边长是( )
 如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且BE=DF,连接EF;作CH⊥EF,连接CE、BH,若BH=8,EF=4$\sqrt{10}$,则正方形ABCD的边长是( )
如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且BE=DF,连接EF;作CH⊥EF,连接CE、BH,若BH=8,EF=4$\sqrt{10}$,则正方形ABCD的边长是( )| A. | 5$\sqrt{2}$ | B. | 6$\sqrt{2}$ | C. | 5$\sqrt{5}$ | D. | 6$\sqrt{5}$ |