题目内容
13．两个相似三角形对应角平分线比为2：3，周长差是25，求较大三角形周长．分析 根据相似三角形的性质求出两个三角形的周长比，列方程计算即可．
解答 解：∵两个相似三角形对应角平分线比为2：3，
∴两个相似三角形的相似比为2：3，
∴两个相似三角形的周长比为2：3，
设较大三角形周长为3x，则较小三角形周长为2x，
由题意得，3x-2x=25，
解得x=25，
则3x=75．
答：较大三角形周长为75．
点评 本题考查的是相似三角形的性质，相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方；相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比．
练习册系列答案
相关题目
3．在平面直角坐标系xOy中，经过点（sin45°，cos30°）的直线，与以原点为圆心，2为半径的圆的位置关系是（ ）
| A． | 相交 | B． | 相切 | ||
| C． | 相离 | D． | 以上三者都有可能 |
8．计算：
（1）（a-4）•$\frac{16-a^2}{a^2-8a+16}$；
（2）$\frac{a^2-a+\frac{1}{4}}{a-3}÷\frac{2a-1}{{a}^{2}-3a}$．
（1）（a-4）•$\frac{16-a^2}{a^2-8a+16}$；
（2）$\frac{a^2-a+\frac{1}{4}}{a-3}÷\frac{2a-1}{{a}^{2}-3a}$．
阿春准备在如图所示的边长为1的正方形网格中，作一个三边长分别为4，5，$\sqrt{17}$的△ABC，他已经作出了其中的一条边，请你帮他把这个三角形补充完整．
20．
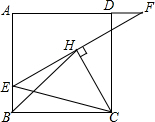如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且BE=DF，连接EF；作CH⊥EF，连接CE、BH，若BH=8，EF=4$\sqrt{10}$，则正方形ABCD的边长是（ ）
如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且BE=DF，连接EF；作CH⊥EF，连接CE、BH，若BH=8，EF=4$\sqrt{10}$，则正方形ABCD的边长是（ ）| A． | 5$\sqrt{2}$ | B． | 6$\sqrt{2}$ | C． | 5$\sqrt{5}$ | D． | 6$\sqrt{5}$ |