题目内容
3. 如图,在正方形ABCD中,点E是边CD上一点,点F是边BC的延长线上一点,连接BE、DF,且BE=DF.
如图,在正方形ABCD中,点E是边CD上一点,点F是边BC的延长线上一点,连接BE、DF,且BE=DF.求证:∠BEC=∠DFC.
分析 直接利用正方形的性质结合HL定理得出Rt△BCE≌Rt△DCF,进而得出答案.
解答 证明:∵四边形ABCD是正方形,
∴BD=DC,∠BCD=90°,
∴∠DCF=90°,
在Rt△BCE和Rt△DCF中,
$\left\{\begin{array}{l}{BC=DC}\\{BE=DF}\end{array}\right.$,
∴Rt△BCE≌Rt△DCF(HL),
∴∠BEC=∠DFC.
点评 此题主要考查了正方形的性质以及全等三角形的判定与性质,正确得出Rt△BCE≌Rt△DCF是解题关键.

练习册系列答案
相关题目
18.用每分可抽30t水的抽水机来抽污水管道内的污水,估计积存的污水超过1200t而不足1500t,则将污水抽完所用时间x的取值范围是( )
| A. | 40<x≤50 | B. | 40≤x<50 | C. | 40<x<50 | D. | 40≤x≤50 |
15.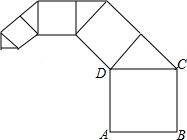 如图,正方形ABCD的边长为1,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S2017的值为( )
如图,正方形ABCD的边长为1,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S2017的值为( )
 如图,正方形ABCD的边长为1,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S2017的值为( )
如图,正方形ABCD的边长为1,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S2017的值为( )| A. | $\frac{1}{{2}^{2014}}$ | B. | $\frac{1}{{2}^{2015}}$ | C. | $\frac{1}{{2}^{2016}}$ | D. | $\frac{1}{{2}^{2017}}$ |
13.随着出行方式的多样化,某地区三类打车方式的收费标准如下:
(如:乘坐8千米,耗时12分钟,出租车的收费为:12+2.4×(8-3)=24(元);滴滴打车的收费为:8×1.5+12×0.5=18(元);神州打车的收费为:8×2+12×0.6=23.2(元))
解决问题:(假设打车的平均车速为30千米/小时)
(1)小明乘车从新街口去南京南站,全程10千米,如果小明使用滴滴打车,需要支付的打车费用为25;
(2)小红乘车从南京博物院去南京青奥公园,用滴滴打车比乘坐出租车节省了3元.求南京博物院到南京青奥公园的路程;
(3)神州打车为了和滴滴打车竞争客户,分别推出了优惠方式,滴滴打车对于乘车路程在5千米以上(含5千米)的客户每次收费立减9元;神舟打车车费5折优惠.对采用哪一种打车方式更合算提出你的建议.
| 出租车 | 滴滴打车 | 神州打车 |
| 3千米以内:12元 | 1.5元/千米 | 2元/千米 |
| 超过3千米的部分:2.4元/千米 | 0.5元/分钟 | 0.6元/分钟 |
解决问题:(假设打车的平均车速为30千米/小时)
(1)小明乘车从新街口去南京南站,全程10千米,如果小明使用滴滴打车,需要支付的打车费用为25;
(2)小红乘车从南京博物院去南京青奥公园,用滴滴打车比乘坐出租车节省了3元.求南京博物院到南京青奥公园的路程;
(3)神州打车为了和滴滴打车竞争客户,分别推出了优惠方式,滴滴打车对于乘车路程在5千米以上(含5千米)的客户每次收费立减9元;神舟打车车费5折优惠.对采用哪一种打车方式更合算提出你的建议.
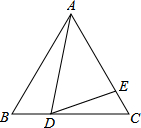 如图,在边长为9的正三角形ABC中,BD=4,∠ADE=60°,则CE的长为$\frac{20}{9}$.
如图,在边长为9的正三角形ABC中,BD=4,∠ADE=60°,则CE的长为$\frac{20}{9}$.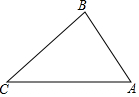 如图,在△ABC中,∠C=45°,∠B=75°,BC=$\sqrt{6}$,求AB的长.
如图,在△ABC中,∠C=45°,∠B=75°,BC=$\sqrt{6}$,求AB的长.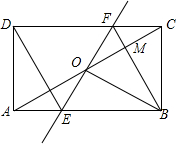 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中一定成立的结论有①③④(将正确结论的序号填在横线上)
如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中一定成立的结论有①③④(将正确结论的序号填在横线上)