题目内容
10.化简:(1)$\frac{4}{a-2}$+a+2
(2)($\frac{x-2}{x+2}$-$\frac{x+2}{x-2}$)$\frac{{x}^{2}-2x}{{x}^{2}}$.
分析 根据分式的运算法则即可求出答案.
解答 解:(1)原式=$\frac{4}{a-2}$+$\frac{(a-2)(a+2)}{a-2}$
=$\frac{{4+{a^2}-4}}{a-2}$
=$\frac{a^2}{a-2}$
(2)原式=$[{\frac{{{{(x-2)}^2}}}{(x+2)(x-2)}-\frac{{{{(x+2)}^2}}}{(x+2)(x-2)}}]•\frac{x(x-2)}{x^2}$
=$\frac{-8x}{(x+2)(x-2)}•\frac{(x-2)}{x}$
=$\frac{-8}{x+2}$
点评 本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
19.现有相同个数的甲、乙两组数据,经计算得:$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,且S甲2=0.35,S乙2=0.25,比较这两组数据的稳定性,下列说法正确的是( )
| A. | 甲比较稳定 | B. | 乙比较稳定 | C. | 甲、乙一样稳定 | D. | 无法确定 |
15.下列判断正确的是( )
| A. | 若一个数的绝对值是它的相反数,则这个数为负数 | |
| B. | 任何数的绝对值都是正数 | |
| C. | 两个数的绝对值相等,则这两个数相等 | |
| D. | 一个正数的绝对值一定是正数 |
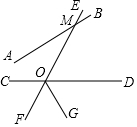 如图,已知直线EF与AB交于点M,与CD交于点O,OG平分∠DOF,若∠COM=120°,∠EMB=$\frac{1}{2}$∠COF.
如图,已知直线EF与AB交于点M,与CD交于点O,OG平分∠DOF,若∠COM=120°,∠EMB=$\frac{1}{2}$∠COF.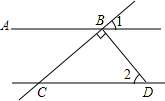 如图,直线AB∥CD,BC⊥BD于点B,∠1=40°,求∠2的度数.
如图,直线AB∥CD,BC⊥BD于点B,∠1=40°,求∠2的度数.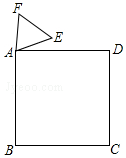 如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小是15°或165°.
如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小是15°或165°.