题目内容
13.已在2a2+b=1,a>0,b>0,求2a+b的最值.分析 由已知条件得到b=2a2-1,则所求的代数式转化为2a2+2a-1的形式,则利用二次函数图象的性质来求最值即可.
解答 解:∵2a2+b=1,a>0,b>0,
∴b=2a2-1>0,则a>$\frac{\sqrt{2}}{2}$或a<-$\frac{\sqrt{2}}{2}$(舍去).
∴2a+b=2a2+2a-1=2(a+$\frac{1}{2}$)2-$\frac{3}{2}$.
设y=2(a+$\frac{1}{2}$)2-$\frac{3}{2}$,则该函数图象的开口方向向上,且对称轴为x=-$\frac{1}{2}$,
∴在a>$\frac{\sqrt{2}}{2}$上y随a的增大而增大,
∴当a=$\frac{\sqrt{2}}{2}$时,y最大=-$\frac{3}{2}$.
点评 本题考查了二次函数的最值.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.

练习册系列答案
相关题目
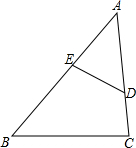 如图,已知D、E分别是△ABC的边AC、AB上的点,若∠A=35°,∠C=85°,∠ADE=60°
如图,已知D、E分别是△ABC的边AC、AB上的点,若∠A=35°,∠C=85°,∠ADE=60° 已知:如图所示,AB=AC,CE=BD,点D、E分别在AB、AC上.
已知:如图所示,AB=AC,CE=BD,点D、E分别在AB、AC上.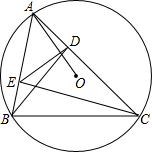 △ABC内接于⊙O,BD、CE为△ABC的两条高,试说明:AO⊥DE.
△ABC内接于⊙O,BD、CE为△ABC的两条高,试说明:AO⊥DE.