题目内容
3.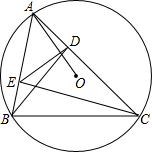 △ABC内接于⊙O,BD、CE为△ABC的两条高,试说明:AO⊥DE.
△ABC内接于⊙O,BD、CE为△ABC的两条高,试说明:AO⊥DE.
分析 延长AO交⊙O于F,连接CF,根据直径所对的圆周角是直角得到∠ACF=90°,根据D、E、B、C四点共圆,得到∠ADE=∠ABC,得到∠ADE+∠FAC=90°,得到答案.
解答  证明:延长AO交⊙O于F,连接CF,
证明:延长AO交⊙O于F,连接CF,
则∠ACF=90°,
∵BD、CE为△ABC的两条高,
∴∠BEC=∠BDC=90°,
∴D、E、B、C四点共圆,
∴∠ADE=∠ABC,又∠AFC=∠ABC,
∴∠ADE=∠AFC,
∴∠ADE+∠FAC=90°,
∴AO⊥DE.
点评 本题考查的是三角形的外接圆、圆周角定理、四点共圆的知识,掌握同弧所对的圆周角相等、直径所对的圆周角是直角是解题的关键.

练习册系列答案
相关题目
 如图,在△ABC与△ABD中,AD与BC相交于0点,∠1=∠2,请你添加一个条件(不再添加其他线段,不再标注或使用其他字母),使AC=BD.并给出证明.
如图,在△ABC与△ABD中,AD与BC相交于0点,∠1=∠2,请你添加一个条件(不再添加其他线段,不再标注或使用其他字母),使AC=BD.并给出证明.