题目内容
12. 在直角坐标系中,直线y=x+2与y轴交于点A1,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C1C2…,A1、A2、A3…在直线y=x+2上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左到右依次记为S1、S2、S3、…Sn,则Sn的值为22n-1(用含n的代数式表示,n为正整数).
在直角坐标系中,直线y=x+2与y轴交于点A1,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C1C2…,A1、A2、A3…在直线y=x+2上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左到右依次记为S1、S2、S3、…Sn,则Sn的值为22n-1(用含n的代数式表示,n为正整数).
分析 结合正方形的性质结合直线的解析式可得出:A2B1=OC1,A3B2=C1C2,A4B3=C2C3,…,结合三角形的面积公式即可得出:S1=$\frac{1}{2}$OC12=2,S2=$\frac{1}{2}$C1C22=8,S3=$\frac{1}{2}$C2C32=32,…,根据面积的变化可找出变化规律“Sn=22n-1(n为正整数)”,依此规律即可得出结论.
解答 解:令一次函数y=x+2中x=0,则y=2,
∴点A1的坐标为(0,2),OA1=2.
∵四边形AnBnCnCn-1(n为正整数)均为正方形,
∴A1B1=OC1=2,A2B2=C1C2=4,A3B3=C2C3=6,….
令一次函数y=x+2中x=2,则y=4,
即A2C1=4,
∴A2B1=A2C1-A1B1=2=A1B1,
∴tan∠A2A1B1=1.
∵AnCn-1⊥x轴,
∴tan∠An+1AnBn=1.
∴A2B1=OC1,A3B2=C1C2,A4B3=C2C3,….
∴S1=$\frac{1}{2}$OC12=2,S2=$\frac{1}{2}$C1C22=8,S3=$\frac{1}{2}$C2C32=32,…,
∴Sn=22n-1(n为正整数).
故答案为:22n-1.
点评 本题考查了一次函数图象上点的坐标特征、正方形的性质、三角形的面积公式的知识,此题属规律性题目,比较复杂.

练习册系列答案
相关题目
2.下列命题是假命题的是( )
| A. | 同弧或等弧所对的圆周角相等 | B. | 平分弦的直径垂直于弦 | ||
| C. | 两条平行线间的距离处处相等 | D. | 直径所对的圆周角等于90° |
3.如图,边长为(m+5)的正方形纸片剪出一个边长为m的正方形之后,剩余部分可剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为5,则另一边长是( )
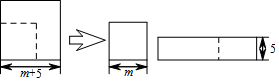

| A. | m+3 | B. | m+5 | C. | 2m+5 | D. | 2m+10 |
7.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4. 如图,直角三角形三边向外作正方形,字母A所代表的正方形的面积为( )
如图,直角三角形三边向外作正方形,字母A所代表的正方形的面积为( )
 如图,直角三角形三边向外作正方形,字母A所代表的正方形的面积为( )
如图,直角三角形三边向外作正方形,字母A所代表的正方形的面积为( )| A. | 4 | B. | 8 | C. | 16 | D. | 64 |
2.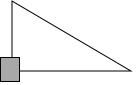 如图所示,小亮数学书上的直角三角形的直角处被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,小亮画出这个三角形的依据是( )
如图所示,小亮数学书上的直角三角形的直角处被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,小亮画出这个三角形的依据是( )
 如图所示,小亮数学书上的直角三角形的直角处被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,小亮画出这个三角形的依据是( )
如图所示,小亮数学书上的直角三角形的直角处被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,小亮画出这个三角形的依据是( )| A. | HL | B. | SAS或AAS | C. | ASA | D. | SSS |
 如图,正方形ABCD的面积为4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为2.
如图,正方形ABCD的面积为4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为2.