题目内容
18.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4,随机摸出一个小球后不放回,再随机摸出一个小球,则两次摸出的小球标号之和等于5的概率为( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸出的小球标号之和等于5的情况,再利用概率公式求解即可求得答案.
解答 解:画树状图得:
∵共有12种等可能的结果,两次摸出的小球标号之和等于5的有4种情况,
∴两次摸出的小球标号之和等于5的概率是:$\frac{4}{12}$=$\frac{1}{3}$.
故选:C.
点评 此题考查了列表法或树状图法求概率.当有两个元素时,可用树形图列举,也可以列表列举.解题时注意:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
9.对于二次函数y=x2-2mx-3,下列结论错误的是( )
| A. | 它的图象与x轴有两个交点 | B. | 方程x2-2mx=3的两根之积为-3 | ||
| C. | 它的图象的对称轴在y轴的右侧 | D. | x<m时,y随x的增大而减小 |
6.下列给出的函数中,其图象是中心对称图形的是( )
①函数y=x;②函数y=x2;③函数y=$\frac{1}{x}$.
①函数y=x;②函数y=x2;③函数y=$\frac{1}{x}$.
| A. | ①② | B. | ②③ | C. | ①③ | D. | 都不是 |
3.7的相反数是( )
| A. | 7 | B. | -7 | C. | $\frac{1}{7}$ | D. | -$\frac{1}{7}$ |
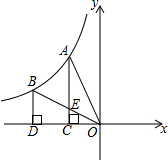 如图,反比例函数y=$\frac{k}{x}(k≠0)$的图象经过A、B两点,过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,连接AO,连接BO交AC于点E,若OC=CD,四边形BDCE的面积为1,则k的值为-$\frac{8}{3}$.
如图,反比例函数y=$\frac{k}{x}(k≠0)$的图象经过A、B两点,过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,连接AO,连接BO交AC于点E,若OC=CD,四边形BDCE的面积为1,则k的值为-$\frac{8}{3}$.