题目内容
6. 观察下面由“☆”组成的图案和算式,解答问题:
观察下面由“☆”组成的图案和算式,解答问题:1+3=4=($\frac{1+3}{2}$)2=22
1+3+5=9=($\frac{1+5}{2}$)2=32
1+3+5+7=16=($\frac{1+7}{2}$)2=42…
(1)请猜想:1+3+5+7+9+…+19的结果是100;
(2)若n表示正整数,请用含n的代数式表示1+3+5+7+9+…+(2n-1)+(2n+1);
(3)请用上述规律计算:21+23+25+…+57+59.
分析 (1)由等式可知左边是连续奇数的和,右边数是1加最后一个奇数一半的平方,由此规律解答即可;
(2)利用(1)的规律得出答案即可;
(3)计算从1加到59这些连续奇数的和,减去从1加到19这些连续奇数的和即可.
解答 解:(1)1+3+5+7+9+…+19=102=100;
(2)由(1)可知1+3+5+7+9+…+(2n-1)+(2n+1)=(n+1)2;
(3)21+23+25+…+57+59
=(1+3+5+…+19+21+23+25+…+57+59)-(1+3+5+…+19)
=302-102
=900-100
=800.
点评 此题主要考查了数字的变化规律,重在发现连续奇数和等于1与最后一个奇数和的一半的平方,利用此规律即可解决问题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
16.下列一元二次方程有实数根的是( )
| A. | x2-2x-2=0 | B. | x2+2x+2=0 | C. | x2-2x+2=0 | D. | x2+2=0 |
14.已知代数式x+2y的值是-3,则代数式2x+4y+1的值是( )
| A. | -6 | B. | -5 | C. | -4 | D. | -3 |
18.若关于x的方程$\frac{3x+a}{x-1}$=1的解是正数,则a的取值范围是( )
| A. | a>-1 | B. | a>-1且a≠0 | C. | a<-1 | D. | a<-1且a≠-3 |
15.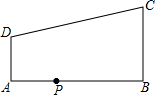 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P的个数有( )
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P的个数有( )
 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P的个数有( )
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.某工艺厂计划一周生产工艺品2100个,平均每天生产300个,但实际每天生产量与计划相比有出入.表是某周的生产情况(超产记为正、减产记为负):
(1)写出该厂星期三生产工艺品的数量;
(2)本周产量中最多的一天比最少的一天多生产多少个工艺品?
(3)请求出该工艺厂在本周实际生产工艺品的数量;
(4)已知该厂实行每周计件工资制,每生产一个工艺品可得60元,若超额完成任务,则超过部分每个另奖50元,少生产一个扣80元.试求该工艺厂在这一周应付出的工资总额.
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减(单位:个) | +5 | -2 | -5 | +15 | -10 | -6 | -9 |
(2)本周产量中最多的一天比最少的一天多生产多少个工艺品?
(3)请求出该工艺厂在本周实际生产工艺品的数量;
(4)已知该厂实行每周计件工资制,每生产一个工艺品可得60元,若超额完成任务,则超过部分每个另奖50元,少生产一个扣80元.试求该工艺厂在这一周应付出的工资总额.
 将连续的整数1,2,3,4,…排列成如下的数表,用3×3正方形框框出9个数(如图).
将连续的整数1,2,3,4,…排列成如下的数表,用3×3正方形框框出9个数(如图).