题目内容
18．若关于x的方程$\frac{3x+a}{x-1}$=1的解是正数，则a的取值范围是（ ）| A． | a＞-1 | B． | a＞-1且a≠0 | C． | a＜-1 | D． | a＜-1且a≠-3 |
分析 先求出方程的解，根据解是正数列出不等式，即可解答．
解答 解：在方程两边同乘x-1得：3x+a=x-1，
解得：x=$\frac{-1-a}{2}$，
∵方程的解是正数，
∴$\left\{\begin{array}{l}{\frac{-1-a}{2}＞0}\\{\frac{-1-a}{2}≠1}\end{array}\right.$
解得a＜-1且a≠-3．
故选：D．
点评 本题考查了分式方程的解、一元一次不等式，解决本题的关键是根据方程的解是正数得出不等式．
练习册系列答案
相关题目
把如图形状的硬纸板折成一个四棱锥，那么与E点重合在一起的是A和C．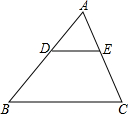
如图，在△ABC中，DE∥BC，AD=2cm，BD=3cm．
观察下面由“☆”组成的图案和算式，解答问题：
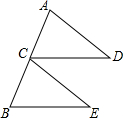如图，已知点C为线段AB的中点，CD=BE，CD∥BE，请判断线段AD与CE的数量关系与位置关系，并说明理由．
10．已知$\frac{a}{2}$=$\frac{b}{5}$，则$\frac{b-a}{a}$的值为（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{2}{5}$ | D． | $\frac{5}{2}$ |
7．如果|a+2|+（b-1）2=0，那么代数式（a+b）2015的值是（ ）
| A． | 1 | B． | -1 | C． | ±1 | D． | 2015 |
如图，在△ABC中，AB=AC，D为BC边上一点，∠B=30°，∠DAB=45°．