题目内容
已知三角形两边分别为6和9，求第三边边上中线的取值范围．
考点：全等三角形的判定与性质,三角形三边关系
专题：
分析：首先根据题意画出图形，求第三边上中线的取值范围，只有将中线与两个已知边转移到同一个三角形中，然后利用三角形的三边关系才能进行分析和判断．
解答：
解：延长AD至M使AD=DM，连接CM．
∵AD为中线，
∴DB=CD，
在△ABD和△CDM中，
，
∴△ABD≌△CDM（SAS），
∴CM=AB=9．
在△ACM中，9-6＜2AD＜9+6，
∴1.5＜AD＜7.5．
解：延长AD至M使AD=DM，连接CM．∵AD为中线，
∴DB=CD，
在△ABD和△CDM中，
|
∴△ABD≌△CDM（SAS），
∴CM=AB=9．
在△ACM中，9-6＜2AD＜9+6，
∴1.5＜AD＜7.5．
点评：本题考查了全等三角形的判定与性质、三角形的三边关系．三角形问题中涉及中线（中点）时，将三角形中线延长一倍，构造全等三角形是常用的解题思路．
练习册系列答案
全能测控期末小状元系列答案
相关题目
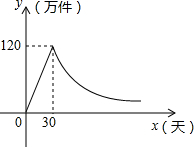某种商品上市之初采用了大量的广告宣传，其销售量与上市的天数之间成正比，当广告停止后，销售量与上市的天数之间成反比（如图），现己知上市30天时，当日销售量为120万件．
实数a在数轴上的位置如图所示，则