题目内容
已知多项式x2＋a能用平方差公式在有理数范围内分解因式，那么在下列四个数中a可以等于( )
A. 9 B. 4
C. －1 D. －2
C
【解析】当x=-1时，x2-1=（x+1）（x-1），其它的三个选项都不符合要求，故选C.
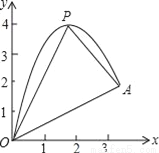
阅读快车系列答案如图，一小球从斜坡O点处抛出，球的抛出路线可以用二次函数y=﹣x2+4x刻画，斜坡可以用一次函数y=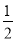
x刻画．
（1）请用配方法求二次函数图象的最高点P的坐标；
（2）小球的落点是A，求点A的坐标；
（3）连接抛物线的最高点P与点O、A得△POA，求△POA的面积；
（4）在OA上方的抛物线上存在一点M（M与P不重合），△MOA的面积等于△POA的面积．请直接写出点M的坐标．
（1）最高点P的坐标为（2，4）；（2）点A的坐标为（， ）；（3）；（4）点M的坐标为（， ）
【解析】试题分析：（1）利用配方法抛物线的一般式化为顶点式，即可求出二次函数图象的最高点P的坐标；
（2）联立两解析式，可求出交点A的坐标；
（3）作PQ⊥x轴于点Q，AB⊥x轴于点B．根据S△POA=S△POQ+S△梯形PQBA﹣S△BOA，代入数值计算即可求解；
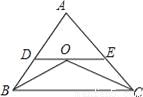
（4）过P... 已知：如图，△ABC中，BO，CO分别是∠ABC和∠ACB的平分线，过O点的直线分别交AB、AC于点D、E，且DE∥BC．若AB=6cm，AC=8cm，则△ADE的周长为__．
14cm
【解析】两直线平行，内错角相等，以及根据角平分线性质，可得△OBD、△EOC均为等腰三角形，由此把△AEF的周长转化为AC+AB．
【解析】
∵DE∥BC，∴∠DOB=∠OBC，又∵BO是∠ABC的角平分线，∴∠DBO=∠OBC，∴∠DBO=∠DOB，∴BD=OD，同理：OE=EC，
∴△ADE的周长=AD+OD+OE+EC=AD+BD+AE+EC=AB+AC=14c... 下列长度的各组线段中，能组成三角形的是 ( )
A. 4、5、6 B. 6、8、15 C. 5、7、12 D. 3、9、13
A
【解析】根据三角形的三边关系，得
A.4+5>6，能组成三角形，符合题意；
B.6+8<15，不能够组成三角形，不符合题意；
C.5+7=12，不能够组成三角形，不符合题意；
D.3+7<13，不能够组成三角形，不符合题意。
故选：A. 分解因式：4x2－9y2.
(2x＋3y)(2x－3y)
【解析】试题分析：直接利用平方差公式因式分解即可.
试题解析：
4x2－9y2=(2x＋3y)(2x－3y). 广东特产专卖店销售龙眼干，其进价为每斤40元，按每斤60元出售，平均每天可售出100斤，后来经调查发现，单价每降低2元，则平均每天的销售量增加20斤．每斤降价多少元，每天销售额最大？
20元
【解析】
试题分析：根据题意可以列出销售额与销售单价之间的关系式，然后整理为顶点式，即可解答本题．
【解析】
设每斤降价x元，销售额为y元，
y=（60﹣x）（100+）=﹣10（x﹣25）2+12250，
∴当x＜25时，y随x的增大而增大，
∵60﹣40=20，
∴0≤x≤20，
∴当x=20时，y取得最大值，
即每斤降价20元时... 某工厂有一种产品现在的年产量是20万件，计划今后两年增加产量，如果每年都比上一年的产量增加x倍，那么两年后这种产品的产量y将随计划所定的x的值而确定，那么y与x之间的关系应表示为_____．
y=20(x+1)2
【解析】∵某工厂一种产品的年产量是20件，每一年都比上一年的产品增加x倍，
∴一年后产品是：20（1+x），
∴两年后产品y与x的函数关系是：y=20（1+x）2．
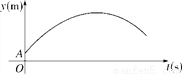
故答案为：y=20（x+1）2. 如图，某足球运动员站在点O处练习射门，将足球从离地面0.5m的A处正对球门踢出(点A在y轴上)，足球的飞行高度y(单位：m)与飞行时间t(单位：s)之间满足函数关系y＝at2＋5t＋c，已知足球飞行0.8s时，离地面的高度为3.5m.
(1)足球飞行的时间是多少时，足球离地面最高？最大高度是多少？
(2)若足球飞行的水平距离x(单位：m)与飞行时间t(单位：s)之间具有函数关系x＝10t，已知球门的高度为2.44m，如果该运动员正对球门射门时，离球门的水平距离为28m，他能否将球直接射入球门？
（1）足球飞行的时间是s时，足球离地面最高，最大高度是4.5m；（2）能.
【解析】试题分析：（1）由题意得：函数y=at2+5t+c的图象经过（0，0.5）（0.8，3.5），于是得到，求得抛物线的解析式为：y=﹣t2+5t+，当t=时，y最大=4.5；
（2）把x=28代入x=10t得t=2.8，当t=2.8时，y=﹣×2.82+5×2.8+=2.25＜2.44，于是得到他能将球直... 和直线l距离为8 cm的直线有______条.
2
【解析】【解析】
在同一平面上，和直线l距离为8cm的直线在直线L的两侧各有一条．故答案为：2．